Funções escalares de várias variáveis
Conjuntos de Nível
Texto sobre conjuntos de nível.
Caderno base da matéria
Vídeoaulas
Acesse o Jamboard da vídeoaula de mapa de contornoExemplos
Vamos agora fazer alguns exemplos. Determine e esboce as curvas de nível das funções dadas abaixo:
a) *(f_{1}(x, y)=x+y)*
Neste caso, observe que *(\operatorname{Dom}\left(f_{1}\right)=\mathbb{R}^{2} \text { e que } \operatorname{Im}\left(f_{1}\right)=\mathbb{R})* e
que *(\operatorname{Im}\left(f_{1}\right)=\mathbb{R})*. Desta forma, temos que para todo *(k)* real, o conjunto de nível *(k)* de *(f1)* é dado por
*(C_{k}\left(f_{1}\right)=\left\{(x, y) \in \mathbb{R}^{2} \mid x+y=k\right\})* Ou seja, as curvas de nível *(k)* de *(f_{1})* são retas *(x + y = k)*.
Por exemplo,
para *(k = 0)*, temos a reta *(y = −x)*;
para *(k = 1)*, temos a reta *(y = −x + 1)*;
para *(k = 2)*, temos a reta *(y = −x + 2)*;
para *(k = −1)*, temos a reta *(y = −x − 1)*;
para *(k = −2)*, temos a reta *(y = −x − 2)*.
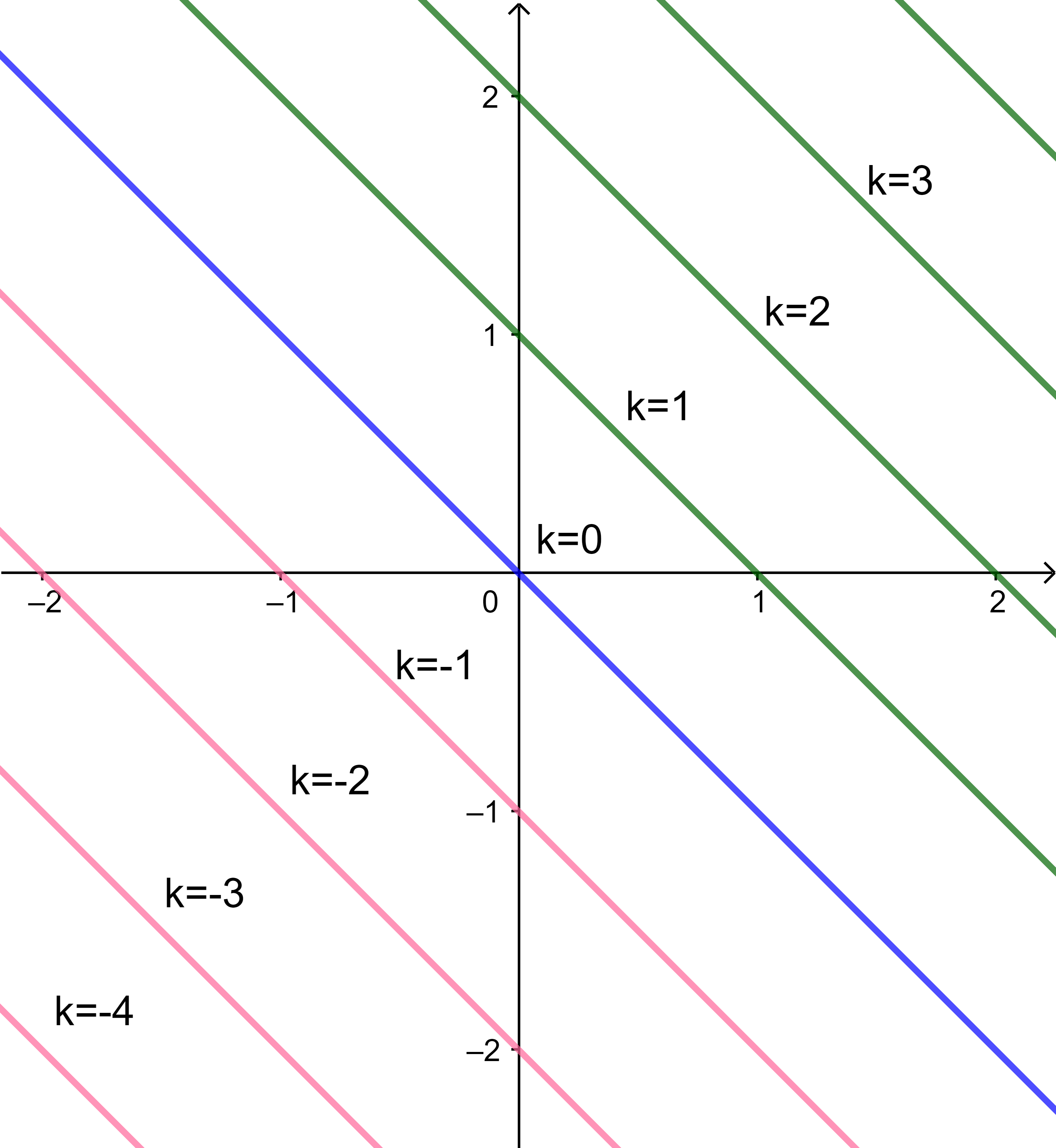
As curvas de nível de *(f_1)* encontram-se esboçadas abaixo. A curva de nível *(k = 0)* está esboçada em azul, as curvas de nível *(k > 0)* estão esboçadas
em verde e as curvas de nível *(k < 0)* estão esboçadas em rosa.
Neste caso, observe que *(\operatorname{Dom}\left(f_{2}\right)=\mathbb{R}^{2} \text { e que } \operatorname{Im}\left(f_{2}\right)=\{z \in \mathbb{R} \mid z \geq 0\})*
Desta forma, temos que, para todo *(k \geq 0)* real, o conjunto de nível *(k)* de *(f_{2})* é dado por *(C_{k}\left(f_{2}\right)=\left\{(x, y) \in \mathbb{R}^{2} \mid x^{2}+y^{2}=k\right\})*.
Oberserve que, para *(k = 0)*, temos apenas o ponto *((0,0))*, então *(C_{0}\left(f_{2}\right)=\{(0,0)\})*. Já para *(k > 0)*, temos que as curvas de nível *(k>0)* de *(k>0)*
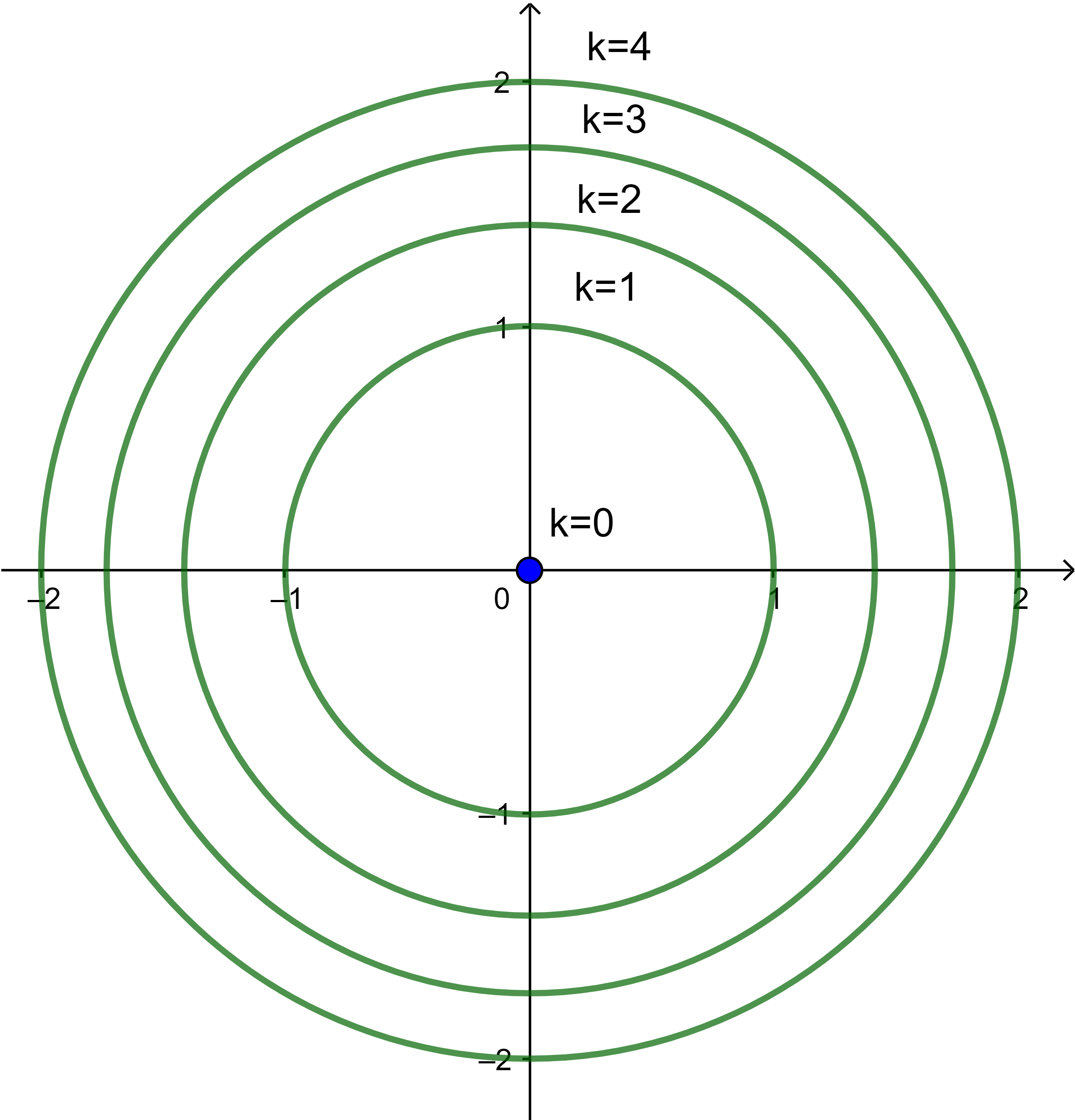
são circunferências *(x^{2}+y^{2}=k)*, circunferências de raio *(\sqrt{k})* e centro na origem. Por exemplo,
para *(k = 1)*, temos a circunferência *(x^2 + y^2 = 1)*;
para *(k = 2)*, temos a circunferência *(x^2 + y^2 = 2)*;
para *(k = 3)*, temos a circunferência *(x^2 + y^2 = 3)*;
para *(k = 4)*, temos a circunferência *(x^2 + y^2 = 4)*.
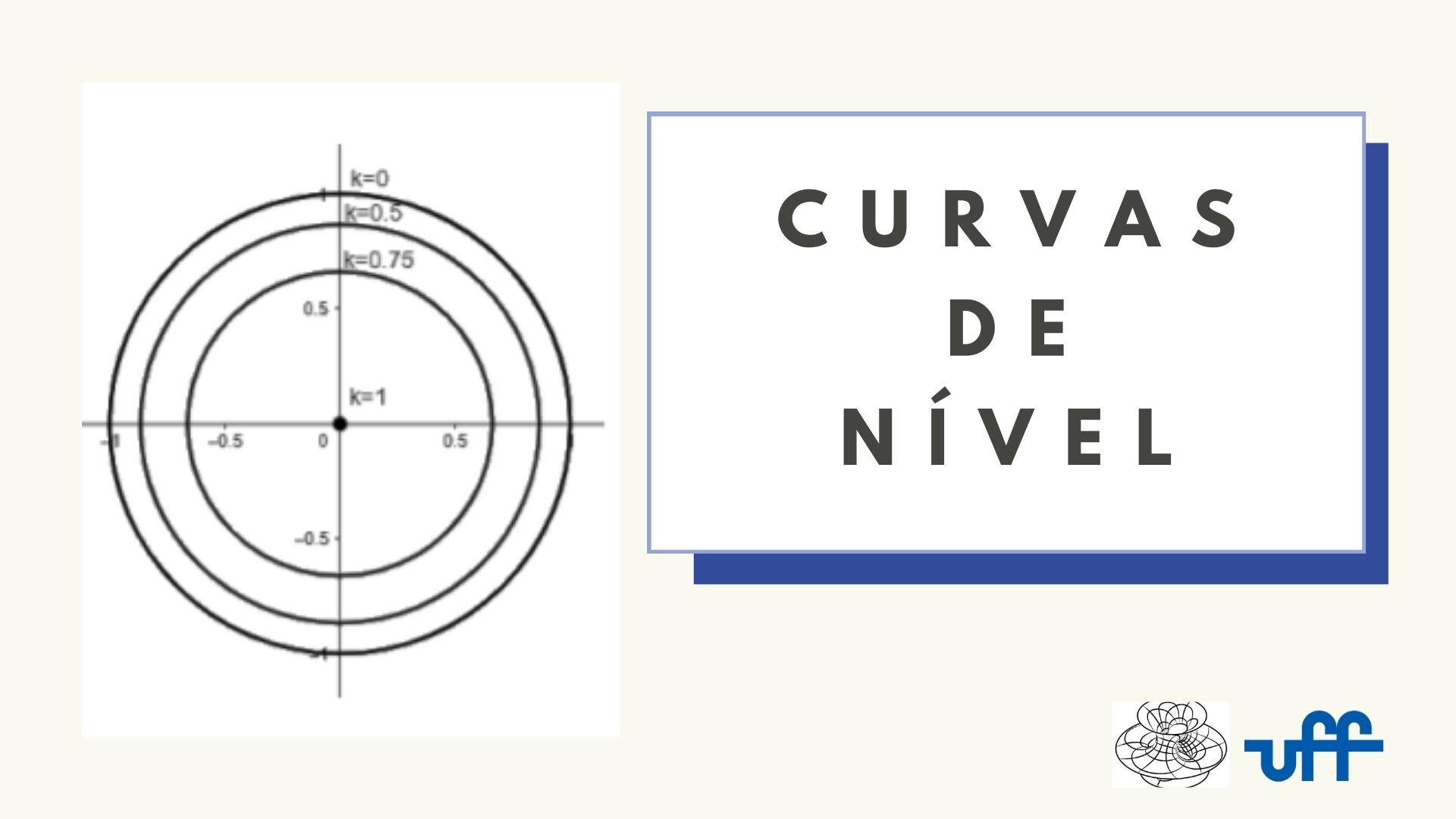
As curvas de nível de *(f_{2})* encontram-se esboçadas abaixo. A curva de nível *(k = 0)* (a origem) está esboçada em azul e as curvas de nível *(k > 0)* estão esboçadas em verde.
Neste caso, observe que *(\operatorname{Dom}\left(f_{3}\right)=\mathbb{R}^{2})* e que *(\operatorname{Im}\left(f_{3}\right)=\mathbb{R})*.Desta forma, temos
que para todo *(k)* real, o conjunto de nível *(k)* de *(f_{3})* é dado por *(C_{k}\left(f_{3}\right)=\left\{(x, y) \in \mathbb{R}^{2} \mid y^{2}-x^{2}=k\right\})*.
Observe que, para *(k = 0)*, temos que *(y^{2}-x^{2}=0 \Leftrightarrow y^{2}=x^{2} \Leftrightarrow|y|=|x| \Leftrightarrow y=x)* ou *(y = −x)*, e as curvas de nível
zero são as retas *(y = x)* e *(y = −x)*. Já para *(k > 0)*, temos que as curvas de nível *(k > 0)* de *(f_{3})* são as hipérboles *(y^2 − x^2 = k > 0)*, e são hipérboles
cujos focos estão no eixo *(y)*. Contudo, para *(k < 0)*, temos que as curvas de nível *(k < 0)* de *(f_{3})* são as hipérboles *(y^2 − x^2 = k < 0)*, e são hipérboles
cujos focos estão no eixo *(x)*. Por exemplo,
para *(k = 0)*, temos as retas *(y = x)* e *(y = −x)*;
para *(k = 1)*, temos a hipérbole *(y^2 − x^2 = 1)*;
para *(k = 2)*, temos a hipérbole *(y^2 − x^2 = 2)*;
para *(k = −1)*, temos a hipérbole *(x^2 − y^2 = 1)*;
para *(k = −2)*, temos a hipérbole *(x^2 − y^2 = 2)*.
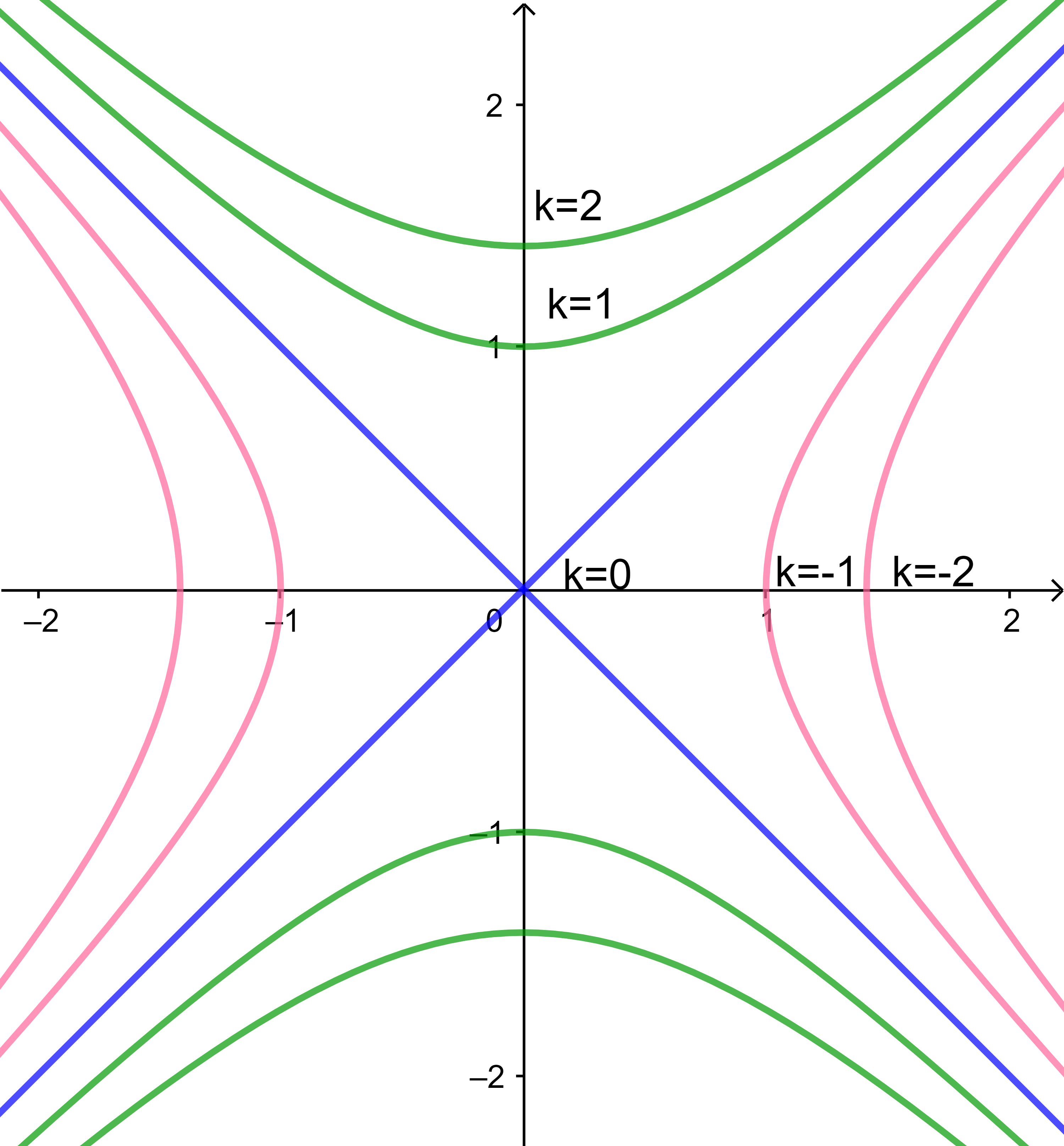
As curvas de nível de *(f_{3})* encontram-se esboçadas abaixo. As curvas de nível *(k = 0)* (retas) estão esboçadas em azul, as curvas de nível *(k > 0)* estão esboçadas em verde
e as curvas de nível *(k < 0)* estão esboçadas em rosa.
Recursos computacionais
Abaixo apresentamos quatro applets sobre curvas de nível e um applet sobre superfície de nível.
Curvas de nível I
Livro Geogebra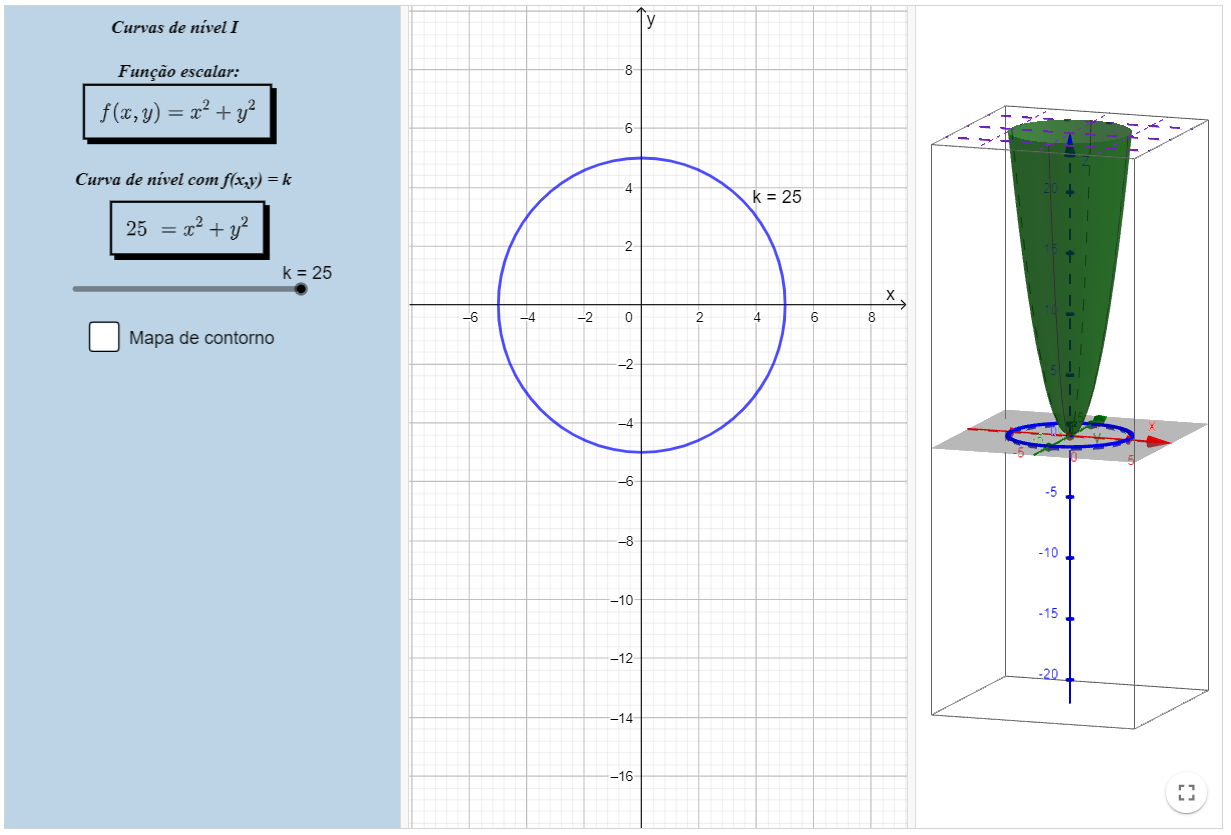
Curvas de nível II
Livro Geogebra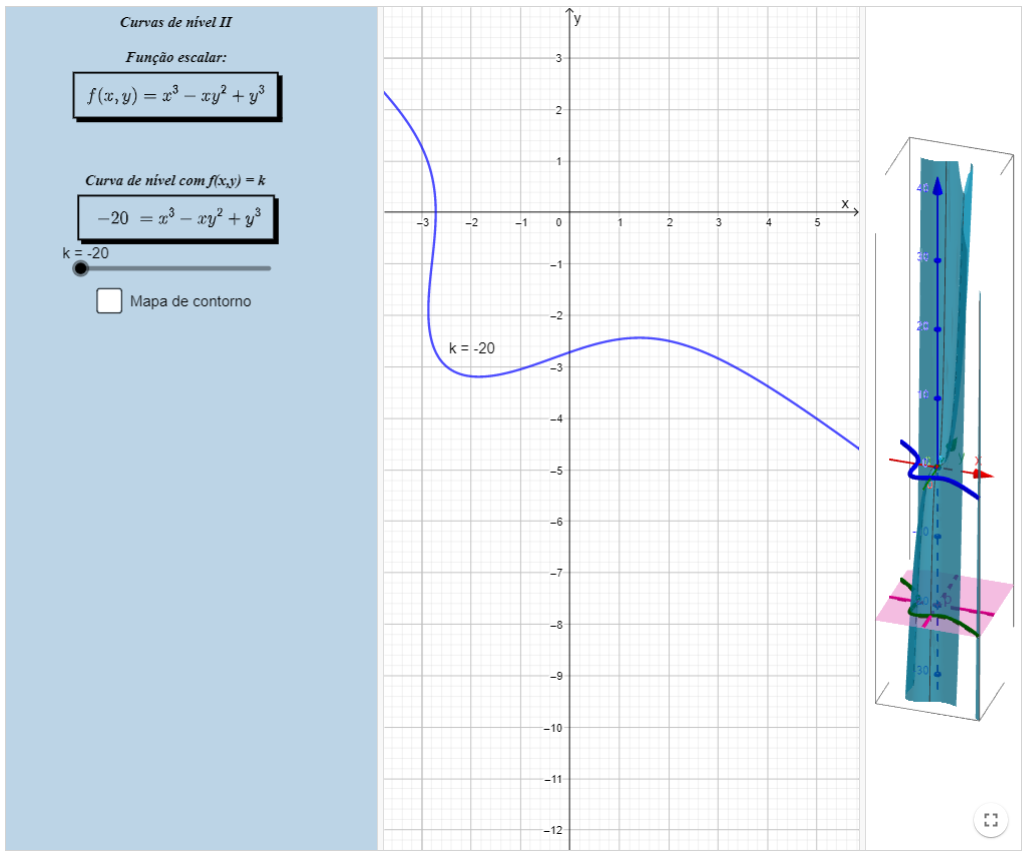
Curvas de nível III
Livro Geogebra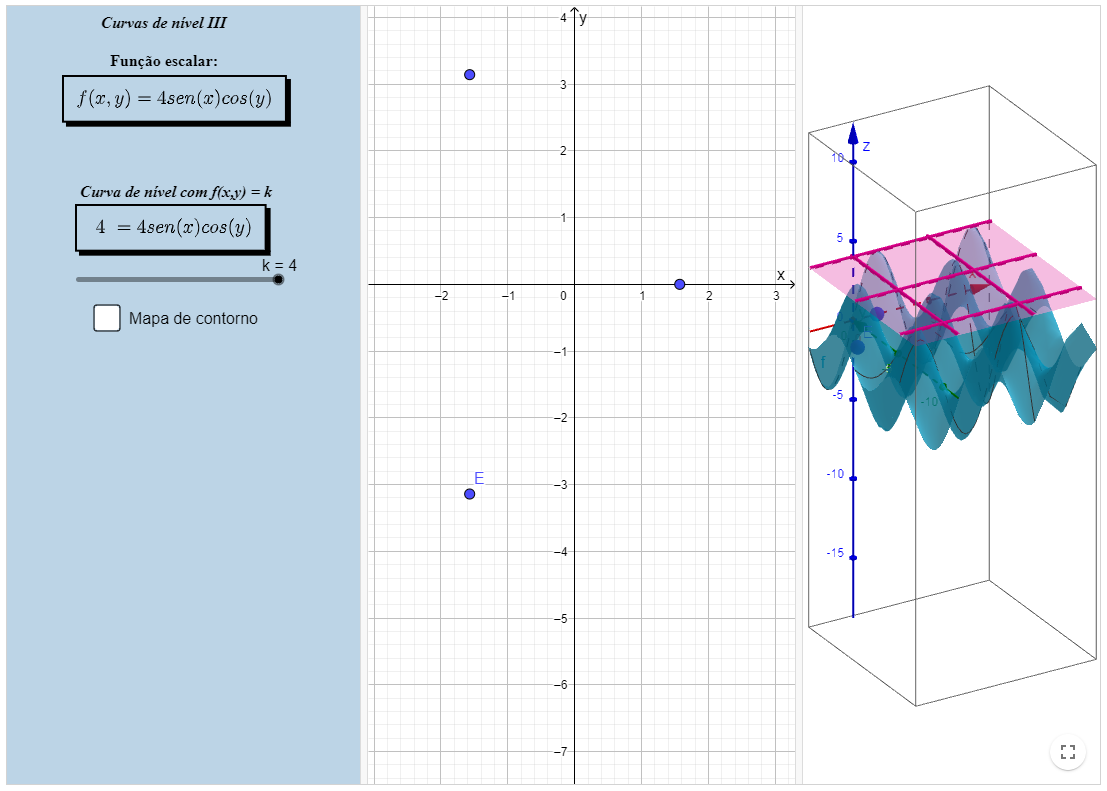
Curvas de nível IV
Livro Geogebra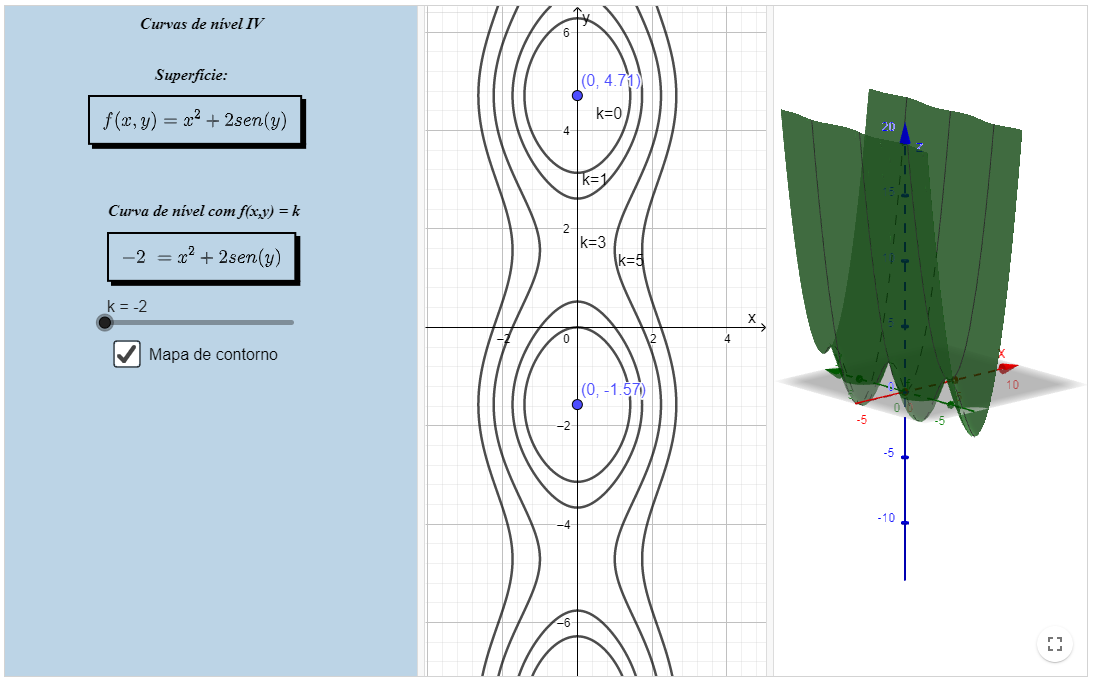
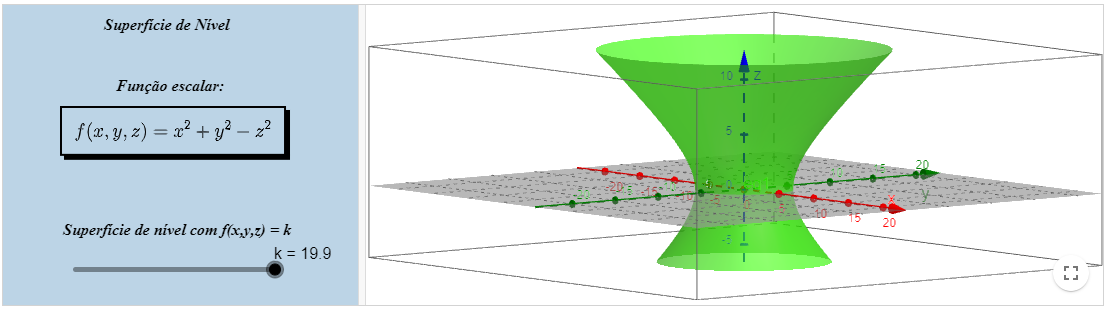
Superfície de nível
Livro Geogebra