Funções vetoriais de uma variável real

Limite de função vetorial
Seja $F$ a função vetorial: $$ \begin{gathered} F: D \subseteq \mathbb{R} \longrightarrow \mathbb{R}^{m} \\ t \mapsto F(t)=\left(f_{1}(t), f_{2}(t), \ldots, f_{m}(t)\right) \end{gathered} $$ e seja $L=\left(l_{1}, l_{2}, \ldots, l_{m}\right)$. Suponha que $F$ está definida em um intervalo aberto contendo o ponto $t_{0}$ (exceto possivelmente no próprio ponto $t=t_{0}$ ). Então, temos que: $$ \lim _{t \longrightarrow t_{0}} F(t)=L \Longleftrightarrow \lim _{t \longrightarrow t_{0}} f_{i}(t)=l_{i}, i=1,2, \ldots, m $$ Portanto, pela expressão acima, temos que: "O limite de $F$, quando $t$ tende a $t_{0}$, existe e é igual a $L=\left(l_{1}, l_{2}, \ldots, l_{m}\right)$ se e somente se o limite de todas as suas coordenadas $f_{i}, i=1,2, \ldots, m$, quando $t$ tende a $t_{0}$, existem e são iguais a $l_{i}, i=1,2, \ldots, m$, respectivamente." A pergunta é... que pode acontecer se um dos limites coordenados não existir?
Nesta seção apresentaremos vários exemplos de limite de função vetorial. O primeiro é o mais simples de todos, onde tudo "se comporta bem". Porém, os seguintes serão mais interessantes de se estudar. Há limite oscilante, infinito, indo para zero, etc.

Limite divergente
Já vimos uma condição para o limite existir (limite convergente). Agora, veremos uma para que o mesmo não exista. $$ \lim _{t \rightarrow t_{0}}\|\vec{r}(t)\|=\infty \Longrightarrow \text { não existe } \lim _{t \rightarrow t_{0}} \vec{r}(t) $$ Isto é, se o módulo do vetor posição tender ao infinito quando $t \rightarrow t_{0}$, então o limite da função vetorial quando $t \rightarrow t_{0}$ não existirá, pois não temos como representar um "vetor com uma das coordenadas (ou várias) sendo infinito", então podemos estudar o limite do vetor posição através do limite do módulo do mesmo. Além disso, é possível que o limite não exista por ser oscilante, da mesma forma que tínhamos em Cálculo de uma variável real, quando tentávamos calcular o limite da função $y=\operatorname{sen}\left(\frac{1}{x}\right)$ quando $x \rightarrow 0$. Ao tentar calcular o limite, nos deparávamos com uma indeterminação deste, pois a função seno oscila indefinidamente tão próxima de $x=0$ quanto se queira. Logo, é possível obtermos algo desse tipo também aqui em funções vetoriais.

Continuidade de função vetorial
Seja $F$ a função vetorial $F: D \subseteq \mathbb{R} \longrightarrow \mathbb{R}^{m}$ e seja $t_{0} \in I($ aberto $) \subseteq D$. Dizemos que $F$ é contínua no ponto $t_{0}$, se: $$ \lim _{t \rightarrow t_{0}} F(t)=F\left(t_{0}\right) $$ Sendo assim, temos que: "F é contínua em to se e somente se todas as funções coordenadas são contínuas em $t_{0} . "$ Dizemos simplesmente que $F$ é contínua se $F$ é contínua para todo $t$ em seu domínio. O caso no qual a função é contínua não é tão interessante de visualizar geometricamente, por se comportar da maneira que gostaríamos. 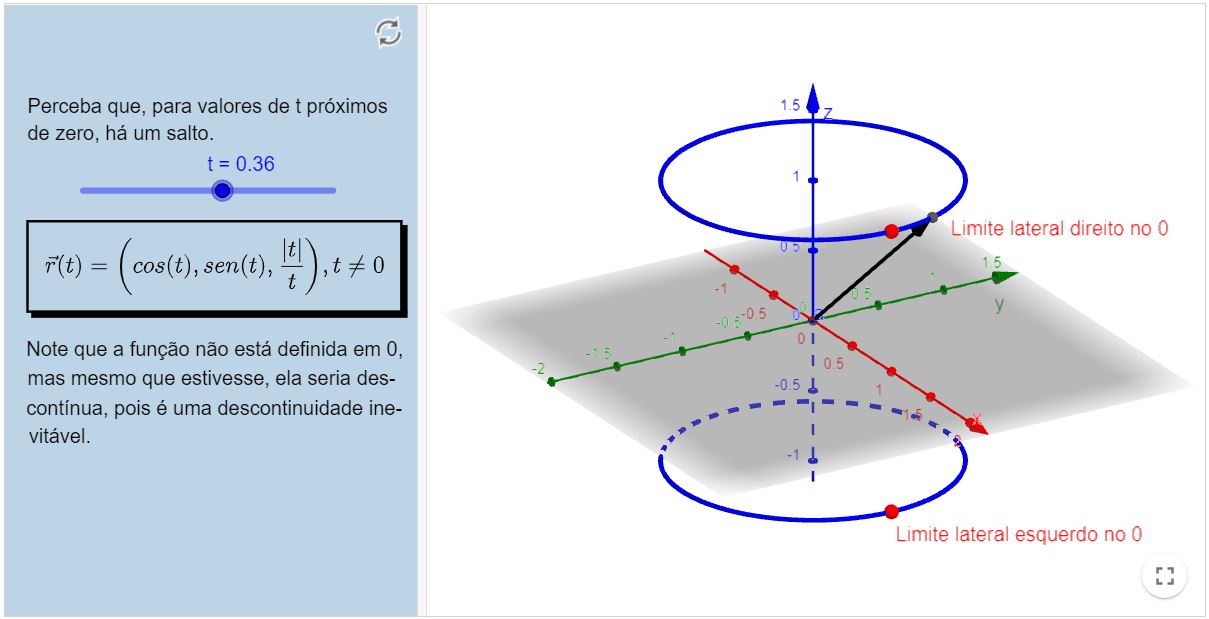Portanto, abaixo você verá um exemplo de função vetorial que é descontínua. Mais precisamente, possui uma descontinuidade de salto. Na figura, estão sinalizados os limites laterais em $t=0$.

Recursos computacionais

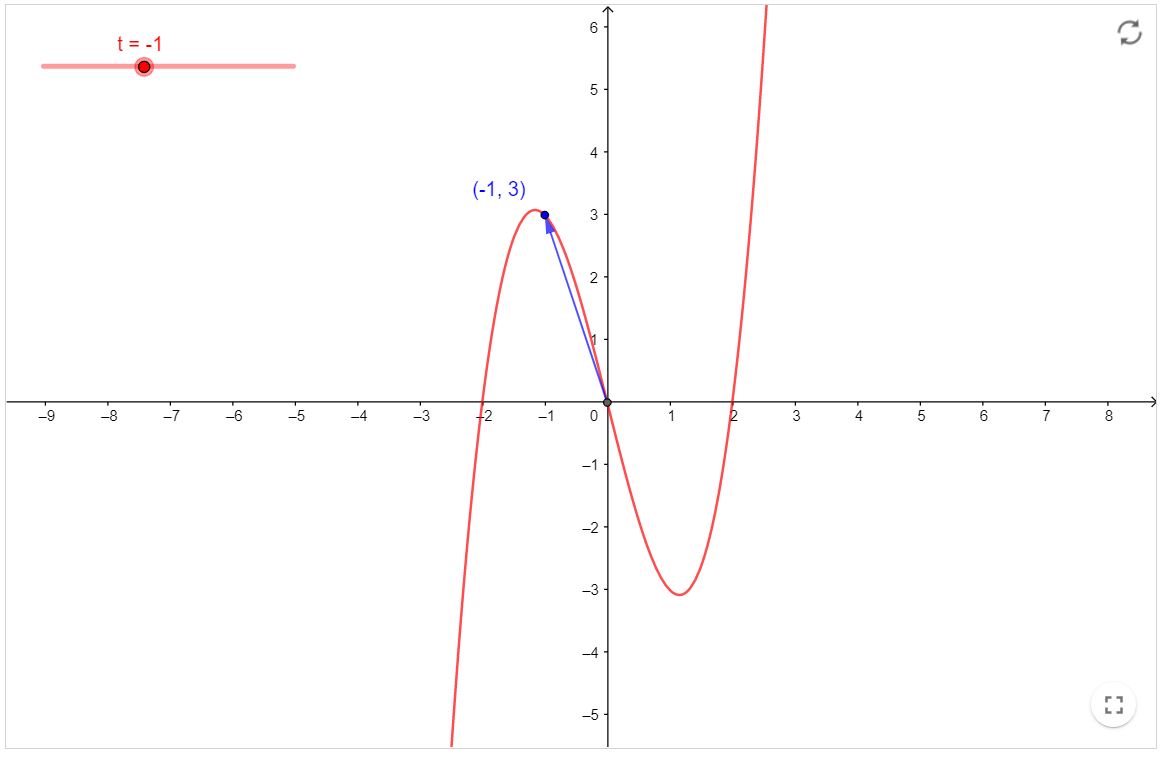
Limite convergente I
Livro Geogebra

Limite convergente II
Livro Geogebra

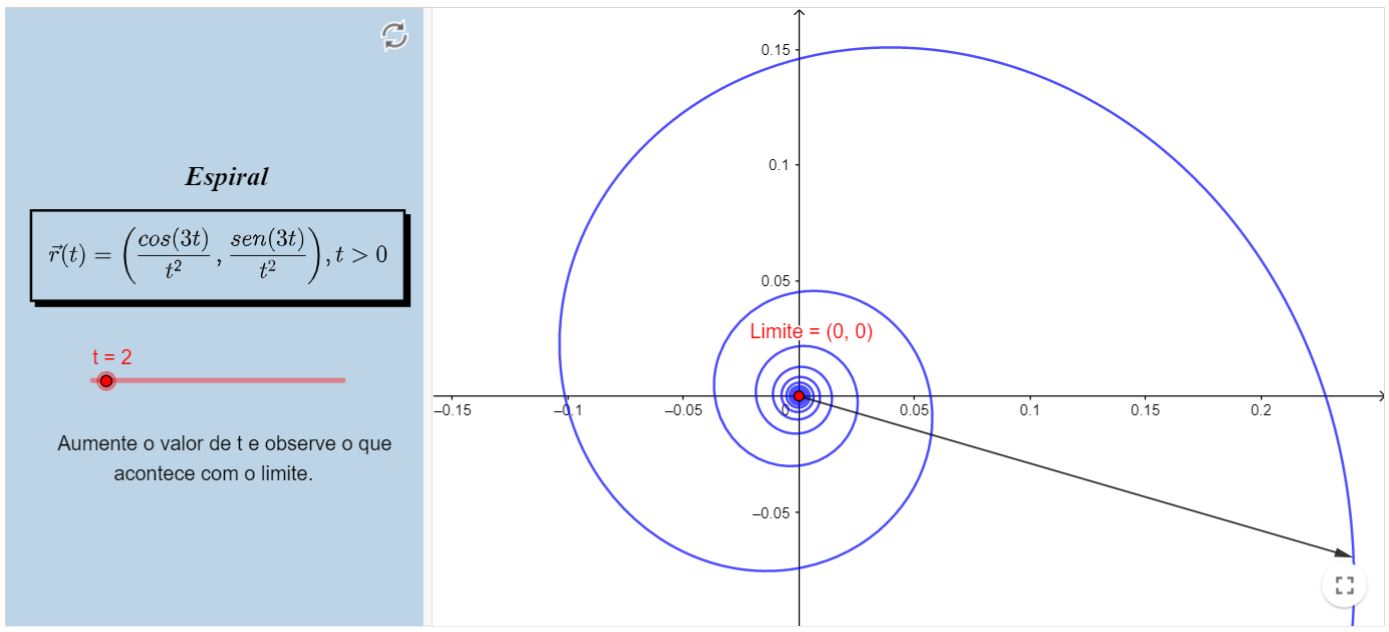
Limite convergente III
Livro Geogebra

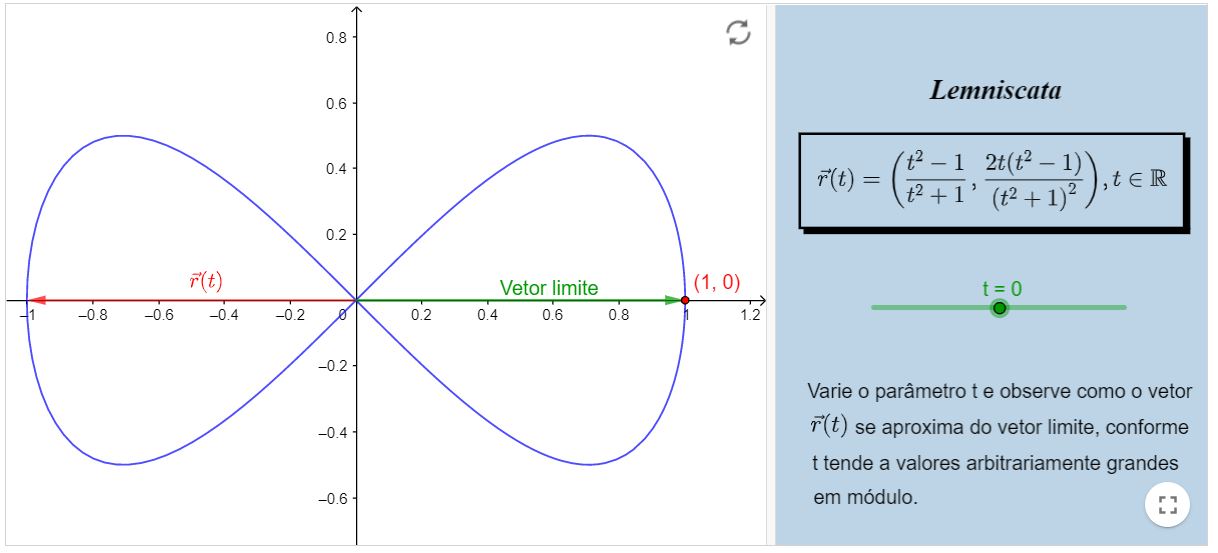
Limite convergente IV
Livro Geogebra

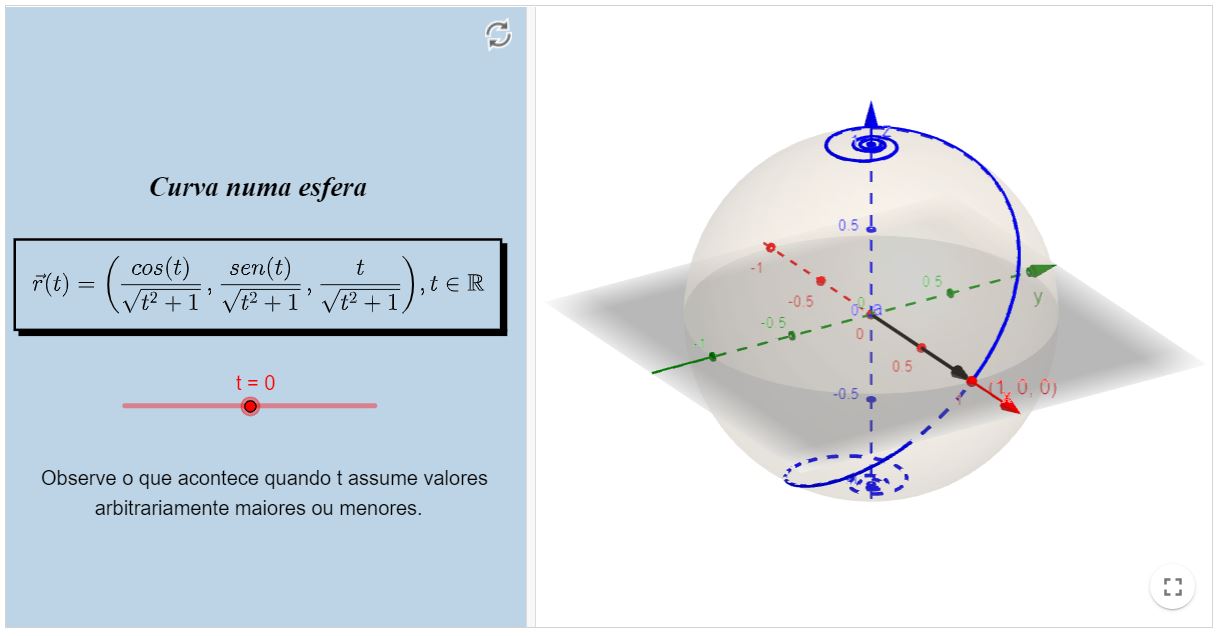
Limite Infinito
Livro Geogebra

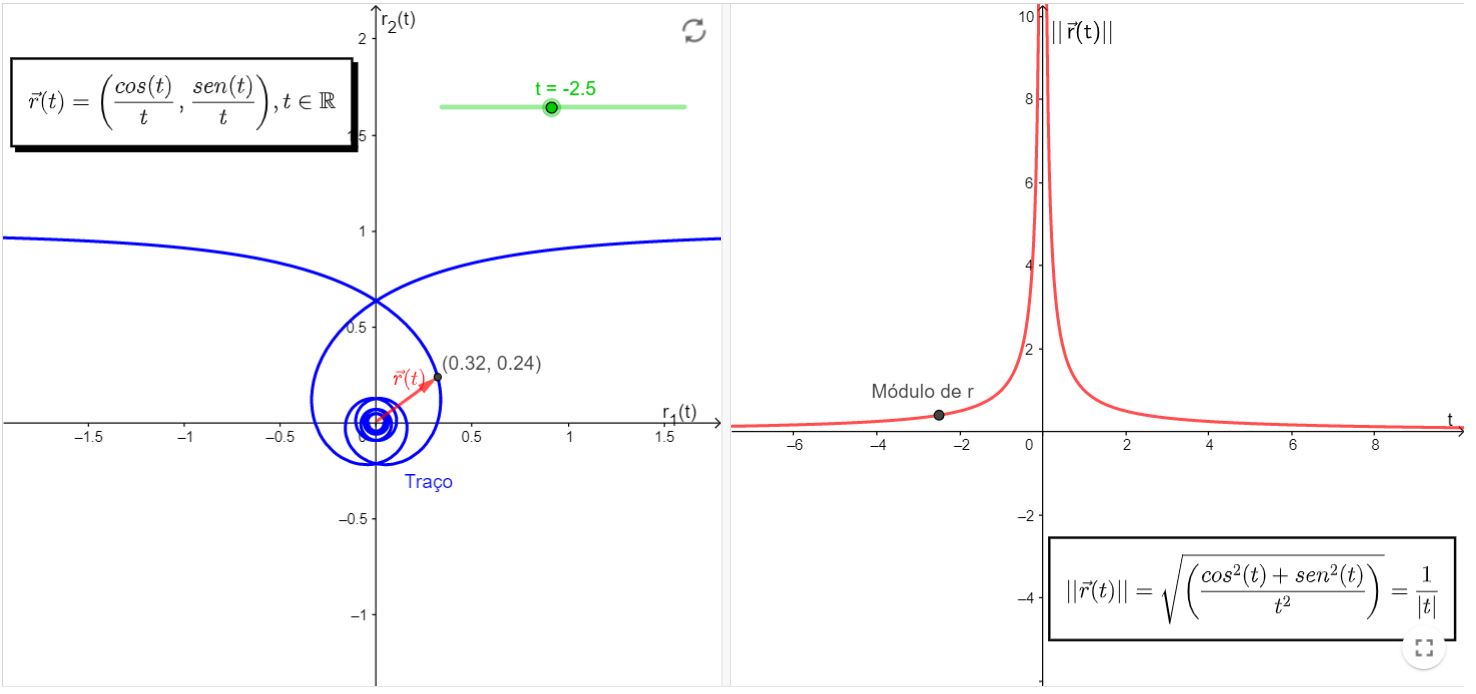
Limite Oscilante
Livro Geogebra

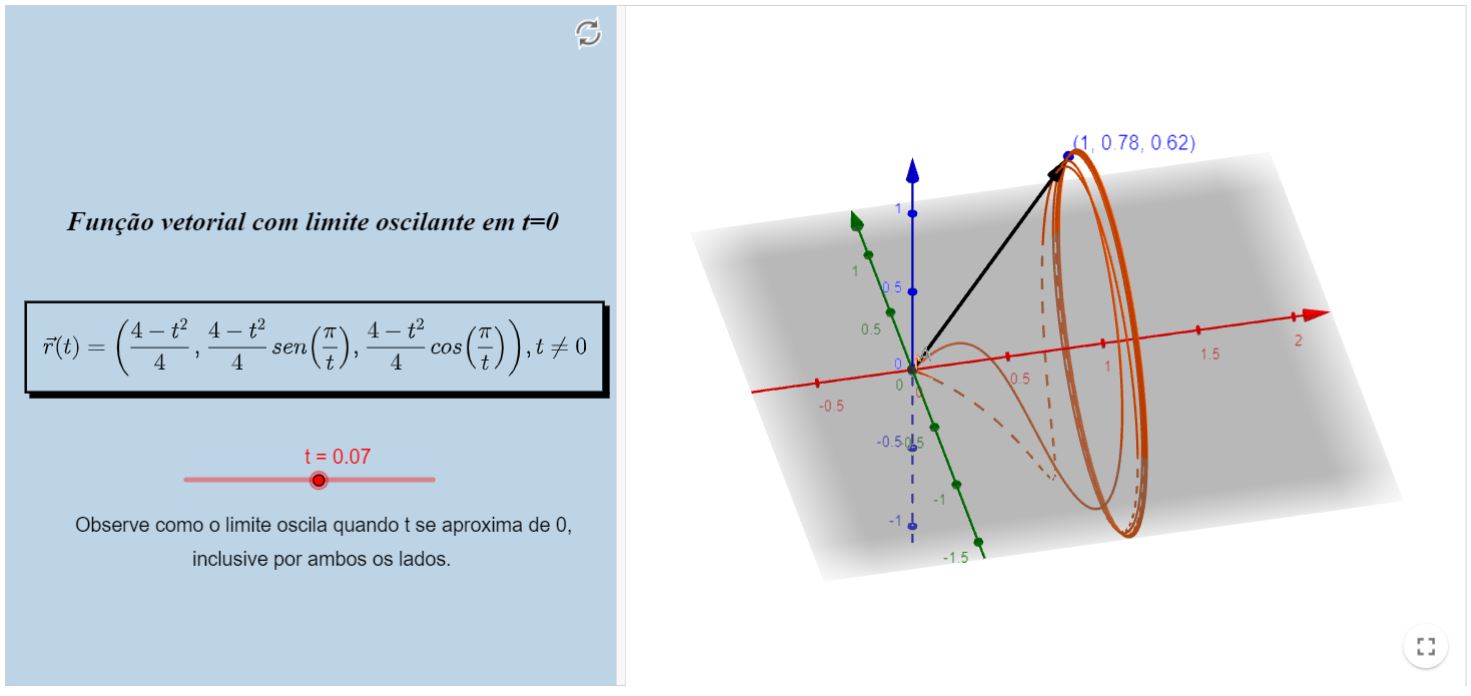
Continuidade de função vetorial
Livro Geogebra