Funções vetoriais de uma variável real

Definição
Uma função vetorial $F$ de uma variável real é uma correspondência, $F: \operatorname{Dom}(F) \subseteq \mathbb{R} \longrightarrow \mathbb{R}^{m}$, que a cada ponto $t \in D o m(F)$, associa um e apenas um $X=\left(x_{1}, x_{2}, \ldots, x_{m}\right) \in \mathbb{R}^{m} .$ O conjunto $\operatorname{Dom}(F)$ é chamado de domínio de $F$ e é o maior conjunto onde $F$ é definida.
Inicialmente apresentaremos exemplos de funções vetoriais com imagem em $\mathbb{R}^{2}$, isto é, $F: \operatorname{Dom}(F) \subseteq \mathbb{R} \rightarrow \mathbb{R}^{2}$, aonde para cada $t \in \operatorname{Dom}(F), F(t)=(x, y)$.
Posteriormente, apresentaremos exemplos de funções vetoriais com imagem em $\mathbb{R}^{3}$, isto é, $F: \operatorname{Dom}(F) \subseteq \mathbb{R} \longrightarrow \mathbb{R}^{3}$, tal que para cada $t \mapsto F(t)=(x, y, z)$, onde $t \in \operatorname{Dom}(F)$. De uma maneira cotidiana, chamamos a função $F$ de $\vec{r}$ ou $r$, como pode-se ver na seção abaixo.

Traço X Gráfico
Não podemos confundir esses dois termos. Considere uma função da forma: $$ F: \operatorname{Dom}(F) \subseteq \mathbb{R} \longrightarrow \mathbb{R}^{2}, \text { tal que } t \mapsto(x(t), y(t)) $$ O conjunto $\operatorname{Im}(F)=\left\{(x(t), y(t)) \in \mathbb{R}^{2} \mid t \in \operatorname{Dom}(F)\right\}$ é chamado conjunto imagem da função vetorial de uma variável $F$. Note que é um conjunto de $\mathbb{R}^{2}$. Por outro lado, o conjunto $G(F)=\left\{(t, x(t), y(t)) \in \mathbb{R}^{3} \mid t \in \operatorname{Dom}(F)\right\}$ representa o gráfico da mesma função. Note que desta vez, o conjunto está em $\mathbb{R}^{3}$, ou seja, diferente da dimensão da imagem.
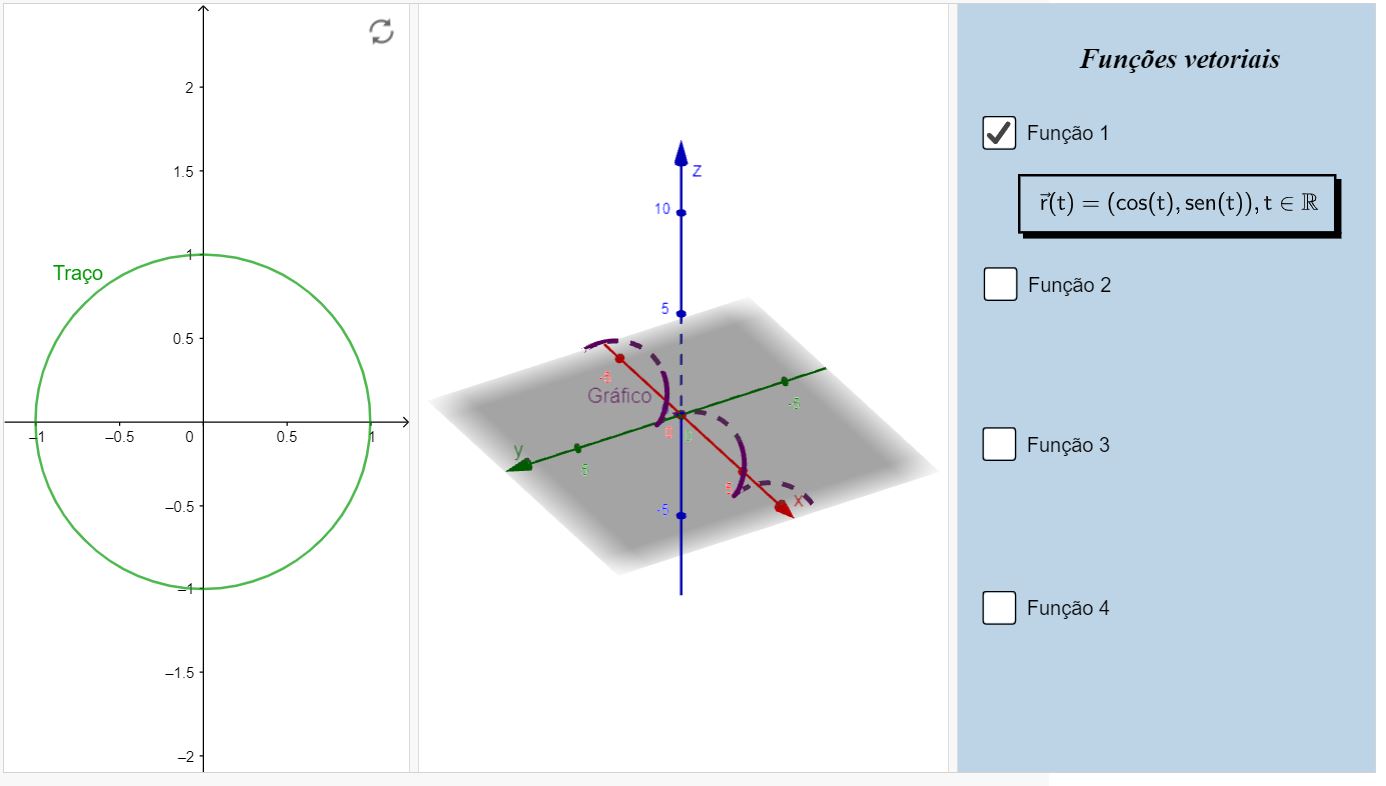
Os exemplos abaixo trazem a ideia abordada nesta seção. Note que na tela da esquerda, está presente a imagem da função vetorial. Por outro lado, na tela direita há o gráfico da mesma função vetorial.

Recursos computacionais

Traço vs Gráfico Os exemplos abaixo trazem a ideia abordada nesta seção. Note que na tela da esquerda, está presente a imagem da função vetorial. Por outro lado, na tela direita há o gráfico da mesma função vetorial.
Livro Geogebra