Revisão de Geometria Analítica

Superfície cilíndrica
É a superfície gerada por uma linha reta (geratriz) que se move, de maneira que é sempre paralela a uma dada reta fixa e passa sempre por um curva fixa (diretriz) dada. No nosso caso, consideraremos a reta fixa apenas como as retas dos eixos coordenados $(O X, O Y$ e $O Z$ ). Observe que, nos exemplos seguintes, cada superfície cilíndrica é gerada por uma curva já familiar (tente identificar qual). Isso significa que estudaremos apenas as superfícies cilíndricas retas. Perceba que as superfícies cilíndricas são um caso especial das quádricas.

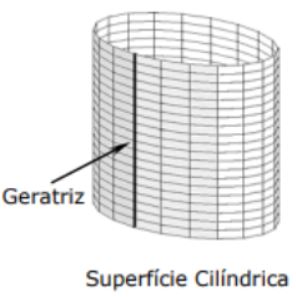
Imagem obtida através do documento em http://www.alunospgmat.ufba.br/adrianocattai/ensino_arquivos/mata01--2006-2/3_superf_cilind.pdf

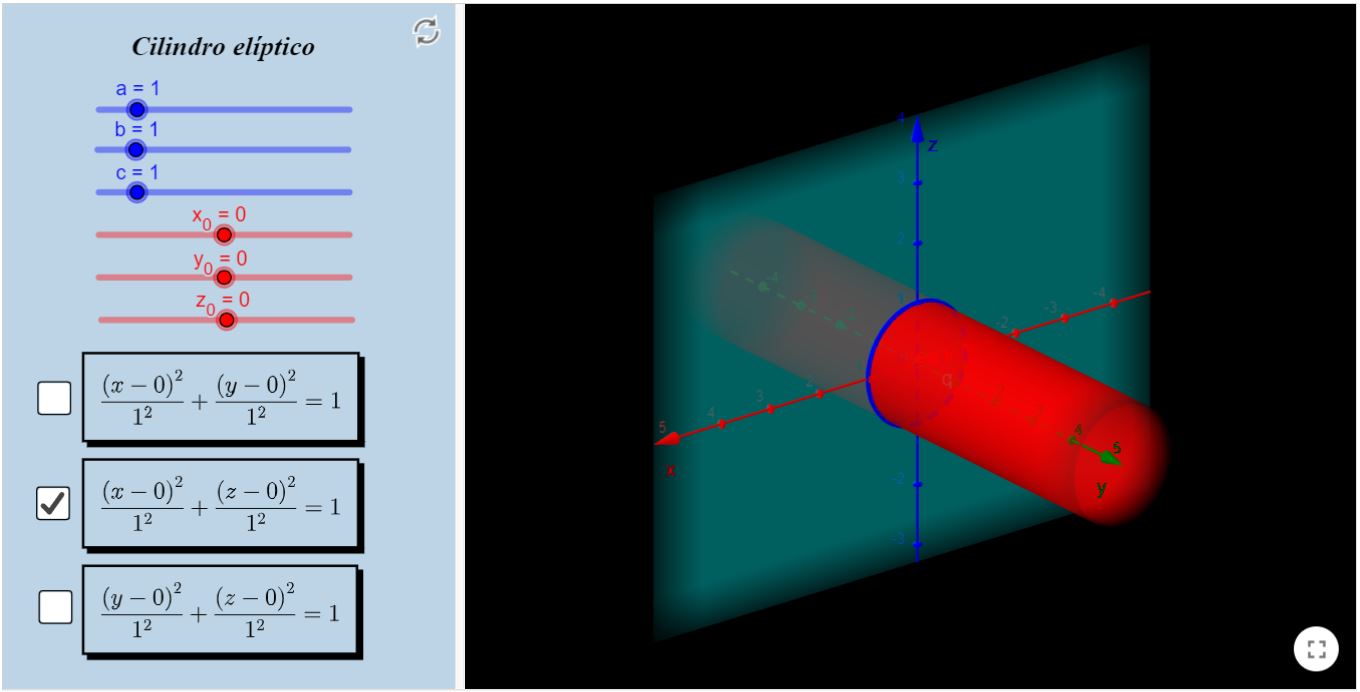
Cilindro Elíptico
As equações que descrevem essa superfície são:
Cilindro elíptico reto em $X Z$ (pode-se considerar a elipse no plano $X Z$ como curva fixa) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \operatorname{com} a, c>0 $$ Repare que quando $a=c$, temos uma circunferência como curva fixa, o que gera um cilindro circular reto. Cilindro elíptico reto em $X Y$ (pode-se considerar a elipse no plano $X Y$ como curva fixa) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}=1, \operatorname{com} a, b>0 $$ Note que se $a=b$, temos uma circunferência como curva fixa, o que gera um cilindro circular reto. Cilindro elíptico reto em $Y Z$ (pode-se considerar a elipse no plano $Y Z$ como curva fixa) $$ \frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \operatorname{com} b, c>0 $$ Novamente, se $b=c$, temos uma circunferência como curva fixa, o que gera um cilindro circular reto. Para nossos fins, talvez não seja imprescindível que o aluno saiba quais são as retas geratrizes, sobretudo porque trabalharemos com as superfícies mais tradicionais, sem muitas complicações, apenas com translações ou dilatações.
No recurso computacional, é possível ver os três diferentes cilindros elípticos que apresentamos aqui.

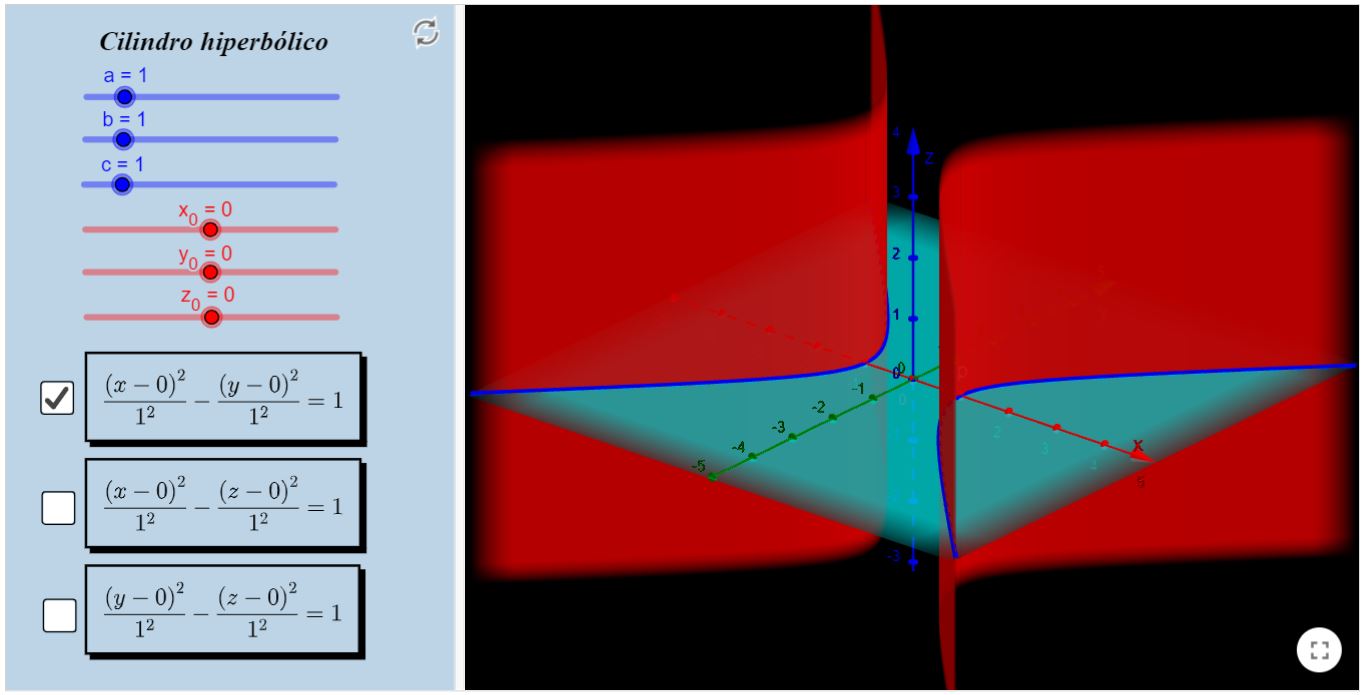
Cilindro Hiperbólico
As equaçoes que descrevem essa superticie são:
Cilindro hiperbólico reto em $X Z$ (pode-se considerar a hipérbole no plano $X Z$ como curva fixa) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \text { com } a, c>0 $$ Cilindro hiperbólico reto em $X Y$ (pode-se considerar a hipérbole no plano $X Y$ como curva fixa) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(y-y_{0}\right)^{2}}{b^{2}}=1, \text { com } a, b>0 $$ Cilindro hiperbólico reto em $Y Z$ (pode-se considerar a hipérbole no plano $Y Z$ como curva fixa) $$ \frac{\left(y-y_{0}\right)^{2}}{b^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \operatorname{com} b, c>0 $$ Para nossos fins, talvez não seja imprescindível que o aluno saiba quais são as retas geratrizes, sobretudo porque trabalharemos com as superfícies mais tradicionais, sem muitas complicações, apenas com translações ou dilatações.
No recurso computacional, é possível ver os três diferentes cilindros hiperbólicos que apresentamos aqui.

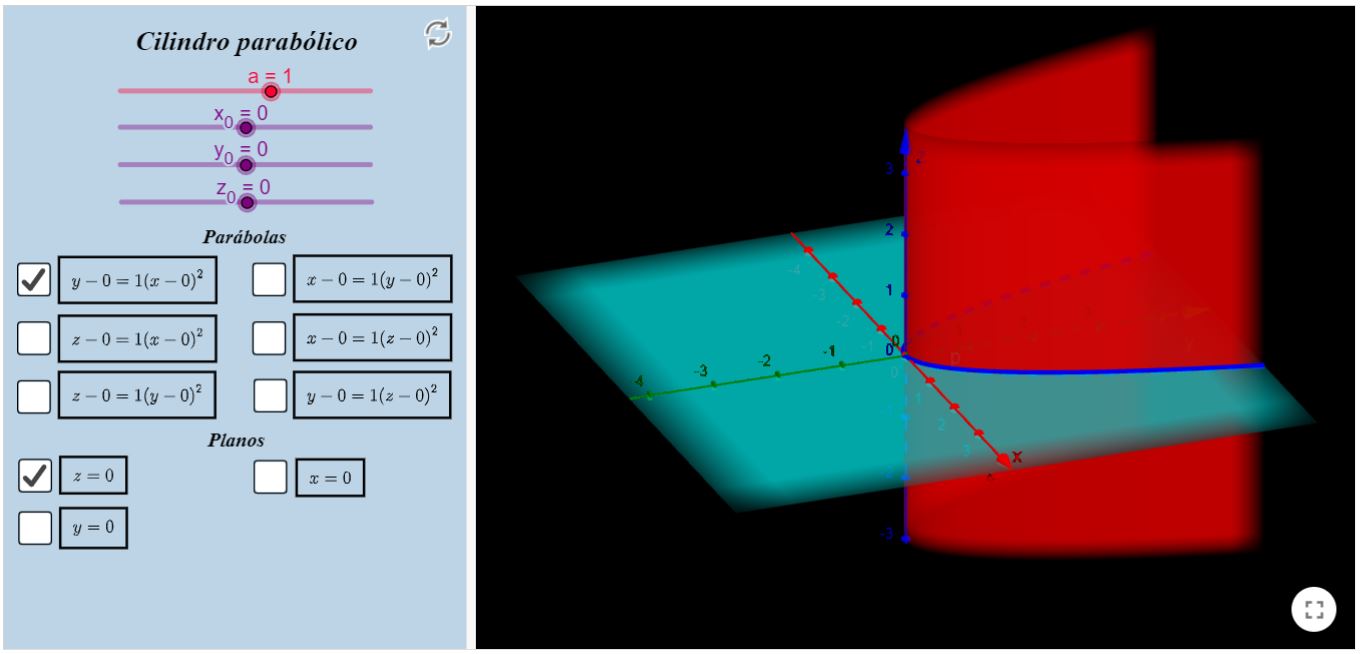
Cilindro Parabólico
As equações que descrevem essa superfície são:
Cilindro parabólico reto em $X Y$ (pode-se considerar a parábola no plano $X Y$ como curva fixa)
$y-y_{0}=a\left(x-x_{0}\right)^{2}$, parábola de $y \mathrm{em} x$ $x-x_{0}=a\left(y-y_{0}\right)^{2}$, parábola de $x$ em $y$

Cilindro parabólico reto em $X Z$ (pode-se considerar a parábola no plano $X Z$ como curva fixa)
$z-z_{0}=a\left(x-x_{0}\right)^{2}$, parábola de $z$ em $x$ $x-x_{0}=a\left(z-z_{0}\right)^{2}$, parábola de $x$ em $z$

Cilindro parabólico reto em $Y Z$ (pode-se considerar a parábola no plano $Y Z$ como curva fixa)
$y-y_{0}=a\left(z-z_{0}\right)^{2}$, parábola de $y \mathrm{em} x$ $z-z_{0}=a\left(y-y_{0}\right)^{2}$, parábola de $z$ em $y$

Uma observação importante é que se $a=0$, teremos apenas os planos coordenados. Para nossos fins, talvez não seja imprescindível que o aluno saiba quais são as retas geratrizes, sobretudo porque trabalharemos com as superfícies mais tradicionais, sem muitas complicações, apenas com translações ou dilatações.
No recurso computacional, é possível ver os seis diferentes cilindros parabólicos que apresentamos aqui.

Recursos computacionais

Cilindro Elíptico
No recurso abaixo, é possível ver os três diferentes cilindros elípticos que apresentamos aqui. Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a, b$ e $c$, eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$ e $z_{0}$.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano, aquele tal que podemos considerar a curva diretriz presente nele. Variando o parâmetro correspondente a esse plano, por exemplo: se selecionar o cilindro elíptico no plano $X Y$, o plano disponível estará associado a $z=z_{0}$. (Pode pensar que é $z=0$ corresponde ao plano $X Y$, e daí você poderá variar esse valor 0 para obter diferentes alturas do plano)
Livro Geogebra

Cilindro Hiperbólico
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção no parâmetro $a$, ele está configurado da mesma forma que fora supracitado, bem como $x_{0}, y_{0}$ e $z_{0}$.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano, aquele tal que podemos considerar a curva diretriz presente nele. Variando o parâmetro correspondente a esse plano, por exemplo: se selecionar o cilindro parabólico no plano $X Y$, o plano disponível estará associado a $z=z_{0}$. (Pode pensar que é $z=0$ corresponde ao plano $X Y$, e daí você poderá variar esse valor 0 para obter diferentes alturas do plano)
Você deve ter reparado que aqui apresentamos o dobro de superfícies em relação ao subtópico anterior. Porém, isso que não quer dizer que não existam outros três cilindros hiperbólicos (é só trocar as variáveis), eles só não são tão frequentes de aparecer. Ademais, visualizar esses cilindros parabólicos é mais confortável visualmente aue o outro caso.
Livro Geogebra

Cilindro Parabólico Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção no parâmetro $a$, ele está configurado da mesma forma que fora supracitado, bem como $x_{0}, y_{0}$ e $z_{0}$.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano, aquele tal que podemos considerar a curva diretriz presente nele. Variando o parâmetro correspondente a esse plano, por exemplo: se selecionar o cilindro parabólico no plano $X Y$, o plano disponível estará associado a $z=z_{0}$. (Pode pensar que é $z=0$ corresponde ao plano $X Y$, e daí você poderá variar esse valor 0 para obter diferentes alturas do plano)
Você deve ter reparado que aqui apresentamos o dobro de superfícies em relação ao subtópico anterior. Porém, isso que não quer dizer que não existam outros três cilindros hiperbólicos (é só trocar as variáveis), eles só não são tão frequentes de aparecer. Ademais, visualizar esses cilindros parabólicos é mais confortável visualmente que o outro caso.
Livro Geogebra