Revisão de Geometria Analítica

De maneira simplificada, uma superfície quádrica pode ser interpretada a partir de um polinômio do segundo grau em três variáveis, isto é, $p(x, y, z)=0$. De fato, uma superfície em $\mathbb{R}^{3}$ pode ser descrita por uma função $F$ de três variáveis, tal que $F(x, y, z)=0$. Para ser uma quádrica, basta que pelo menos um dos monômios tenham grau 2 . No espaço tridimensional, a equação do segundo grau se dá por: $$ A x^{2}+B y^{2}+C z^{2}+D x y+E x z+F y z+G x+H y+I z+J=0 $$ Com $A, B, C, \ldots, J$ constantes reais, onde ao menos um dos coeficientes $A, B, C, D, E$ ou $F$ é não nulo. Simplificando um pouco mais, neste tópico vamos tratar apenas dos casos em que $D, E$ e $F$ são nulos. De fato, ainda que não sejam (teremos uma quádrica rotacionada), podemos fazer uma transformação linear e escrever a equação de forma que esses termos sejam nulos.

Elipsoide
A equação que descrevem essa superfície é: $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1 $$ Note que se $a=b=c$, temos uma esfera (não um elipsoide em si).
No recurso computacional, é possível ver o elipsoide que apresentamos aqui.

Hiperboloide de uma folha
As equações que descrevem essa superfície são:
Hiperboloide de uma folha reto em $z$ (o eixo principal é o eixo $-O Z$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \text { com } a, b, c>0 $$ Hiperboloide de uma folha reto em $y$ (o eixo principal é o eixo $-O Y$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \text { com } a, b, c>0 $$ Hiperboloide de uma folha reto em $x$ (o eixo principal é o eixo $-O X$) $$ -\frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \operatorname{com} a, b, c>0 $$ No recurso computacional, é possível ver os três diferentes hiperboloides de uma folha que apresentamos aqui.

Hiperboloide de duas folhas
As equações que descrevem essa superfície são: Hiperboloide de duas folhas reto em $z$ (o eixo principal é o eixo $-O Z$) $$ -\frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \operatorname{com} a, b, c>0 $$ Hiperboloide de duas folhas reto em $y$ (o eixo principal é o eixo $-O Y$) $$ -\frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \operatorname{com} a, b, c>0 $$ Hiperboloide de duas folhas reto em $x$ (o eixo principal é o eixo $-O X$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(y-y_{0}\right)^{2}}{b^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=1, \text { com } a, b, c>0 $$ No recurso computacional, é possível ver os três diferentes hiperboloides de duas folhas que apresentamos aqui.

Cone Elíptico
As equações que descrevem essa superfície são:
Hiperboloide de uma folha reto em $z$ (o eixo principal é o eixo $-O Z$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=0, \operatorname{com} a, b, c>0 $$ Hiperboloide de uma folha reto em $y$ (o eixo principal é o eixo $-O Y$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=0, \operatorname{com} a, b, c>0 $$ Hiperboloide de uma folha reto em $x$ (o eixo principal é o eixo $-O X$) $$ -\frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=0, \operatorname{com} a, b, c>0 $$ No recurso computacional, é possível ver os três diferentes cones elípticos que apresentamos aqui.

Paraboloide Elíptico
As equações que descrevem essa superfície são
Paraboloide elíptico reto em $z$ (o eixo principal é o eixo $-O Z$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}=c z, \text { com } a, b>0 \text { e } c \neq 0 $$ Paraboloide elíptico reto em $y$ (o eixo principal é o eixo $-O Y$) $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}+\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=b y, \operatorname{com} a, c>0 \text { e } b \neq 0 $$ Paraboloide elíptico reto em $x$ (o eixo principal é o eixo $-O X$) $$ \frac{\left(z-z_{0}\right)^{2}}{c^{2}}+\frac{\left(y-y_{0}\right)^{2}}{b^{2}}=a x, \text { com } b, c>0 \text { e } a \neq 0 $$ No recurso computacional, é possível ver o primeiro paraboloide elíptico que apresentamos aqui (cujo eixo principal é o eixo - $O Z$).

Paraboloide Hiperbolico
As equações que descrevem essa superfície são:
Paraboloide hiperbólico reto em $z$ $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(y-y_{0}\right)^{2}}{b^{2}}=c z, \text { com } a, b>0 \text { e } c \neq 0 $$ Paraboloide hiperbólico reto em $y$ $$ \frac{\left(x-x_{0}\right)^{2}}{a^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=b y, \operatorname{com} a, c>0 \text { e } b \neq 0 $$ Paraboloide hiperbólico reto em $x$ $$ \frac{\left(y-y_{0}\right)^{2}}{b^{2}}-\frac{\left(z-z_{0}\right)^{2}}{c^{2}}=a x, \operatorname{com} b, c>0 \text { e } a \neq 0 $$ Note que se a constante que acompanha a variável do lado direito for positiva, temos um paraboloide hiperbólico e se ela for negativa teremos outro. Logo, no total, temos seis paraboloides hiperbólicos possíveis: dois para cada variável $x, y, z$.
No recurso computacional, é possível ver o primeiro paraboloide hiperbólico que apresentamos aqui (note ao variar $c$, é possível ver dois paraboloides hiperbólicos).

Recursos computacionais

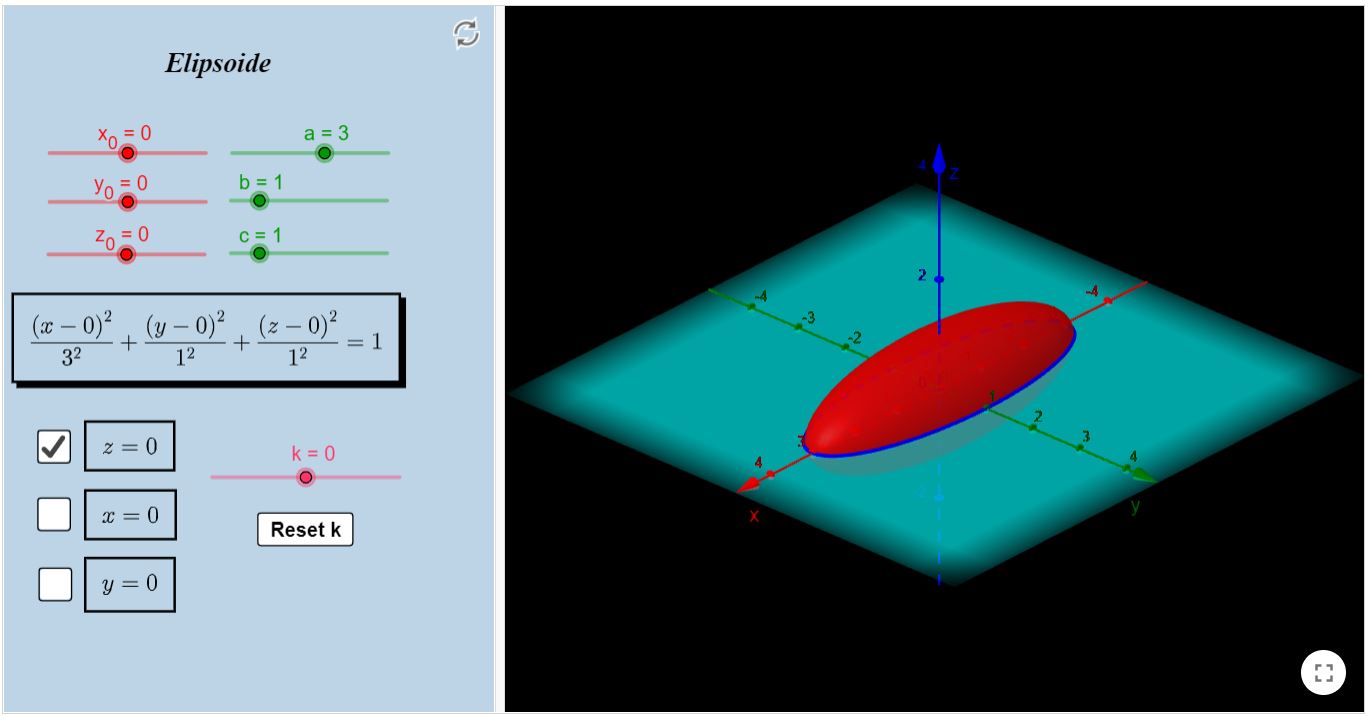
Elipsoide
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a, b$ e $c$, eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$ e $z_{0}$.
Perceba que, junto da superfície, há um plano já selecionado. Você pode variar o parâmetro $k$ para ver as diversas interseções do plano com a superfície (interessante é olhar a forma da curva, você notará que é uma conhecida). Selecione os outros planos também, lembrando sempre de desmarcar o anterior.
Livro Geogebra

Hiperboloide de uma folha
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a, b$ e $c$, eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$ e $z_{0}$.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano que está pré-selecionado. Você pode, para cada plano, selecionar ver a interseção dele com a superfície já selecionada. Para cada opção de hiperboloide, haverá três opções de interseção, cada uma relacionada com o plano que está acima dela. Inclusive poderá "mover" o plano alterando o valor de $k$.

Atenção!!! Para selecionar outra superfície, desmarque TODAS as caixas referentes àquela atual. Caso contrário, as imagens poderão confundilo.

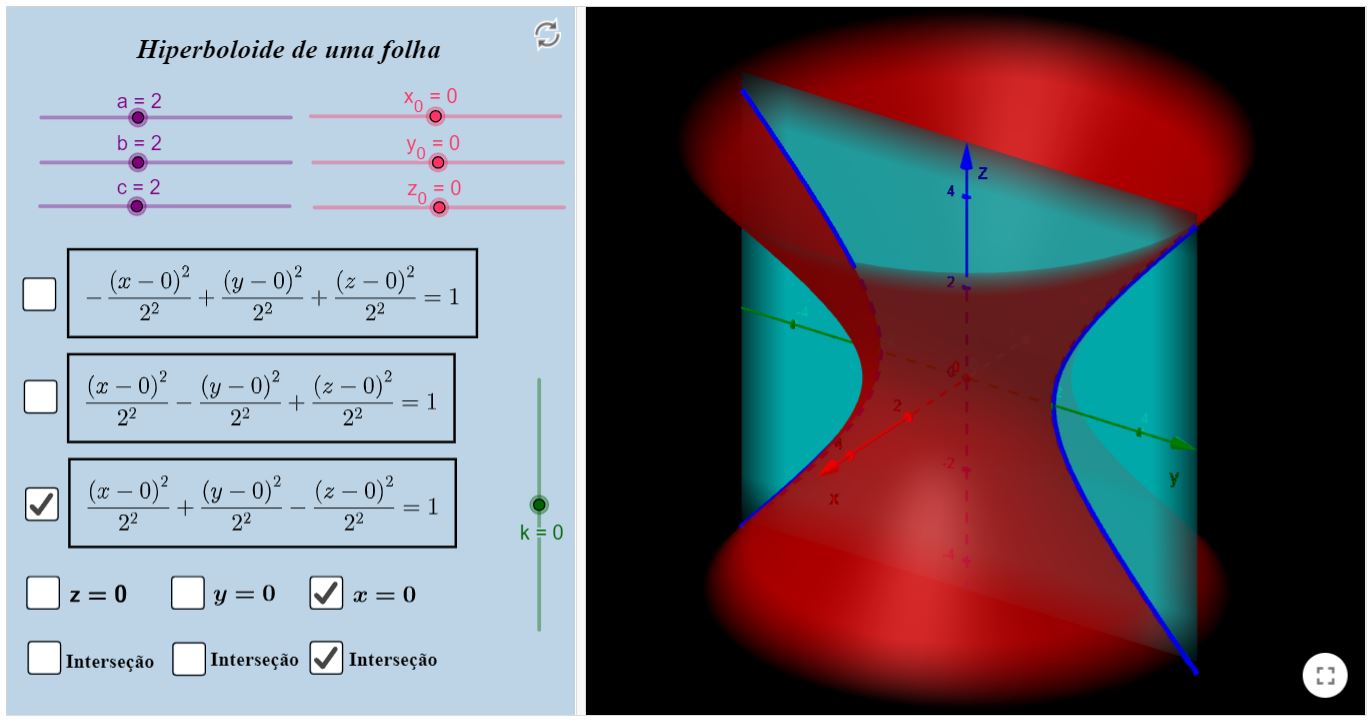
Hiperboloide de duas folhas
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a, b$ e $c$, eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$ e $z_{0}$.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano que está pré-selecionado. Você pode, para cada plano, selecionar ver a interseção dele com a superfície já selecionada. Para cada opção de hiperboloide, haverá três opções de interseção, cada uma relacionada com o plano que está acima dela. Inclusive poderá "mover" o plano alterando o valor de $k$.

Atenção!!! Para selecionar outra superfície, desmarque TODAS as caixas referentes àquela atual. Caso contrário, as imagens poderão confundilo.

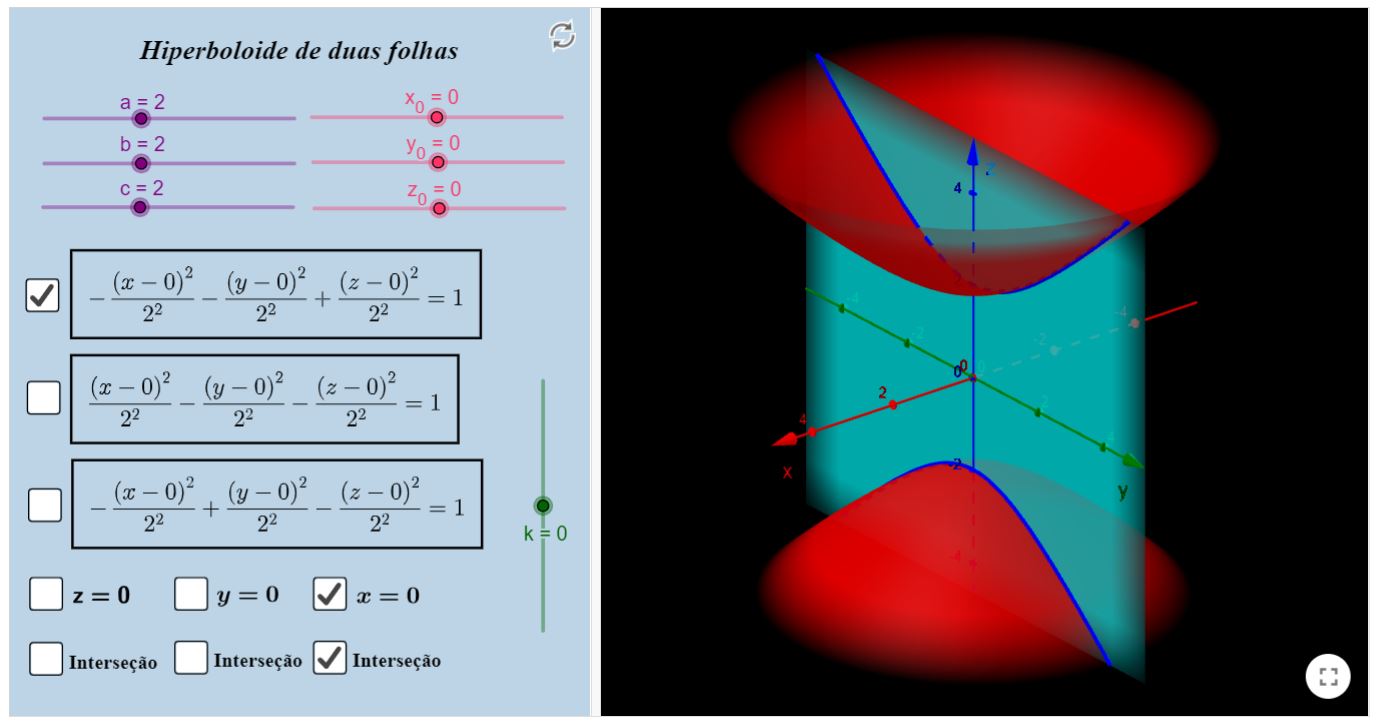
Cone Elíptico
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a, b$ e $c$, eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$ e $z_{0}$. Note que se $a=b=c$, temos o cone circular reto.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano que está pré-selecionado. Você pode, para cada plano, selecionar ver a interseção dele com a superfície já selecionada. Para cada opção de cone, haverá três opções de interseção, cada uma relacionada com o plano que está acima dela. Inclusive poderá "mover" o plano alterando o valor de $k$.

Atenção!!! Para selecionar outra superfície, desmarque TODAS as caixas referentes àquela atual. Caso contrário, as imagens poderão confundi-lo.

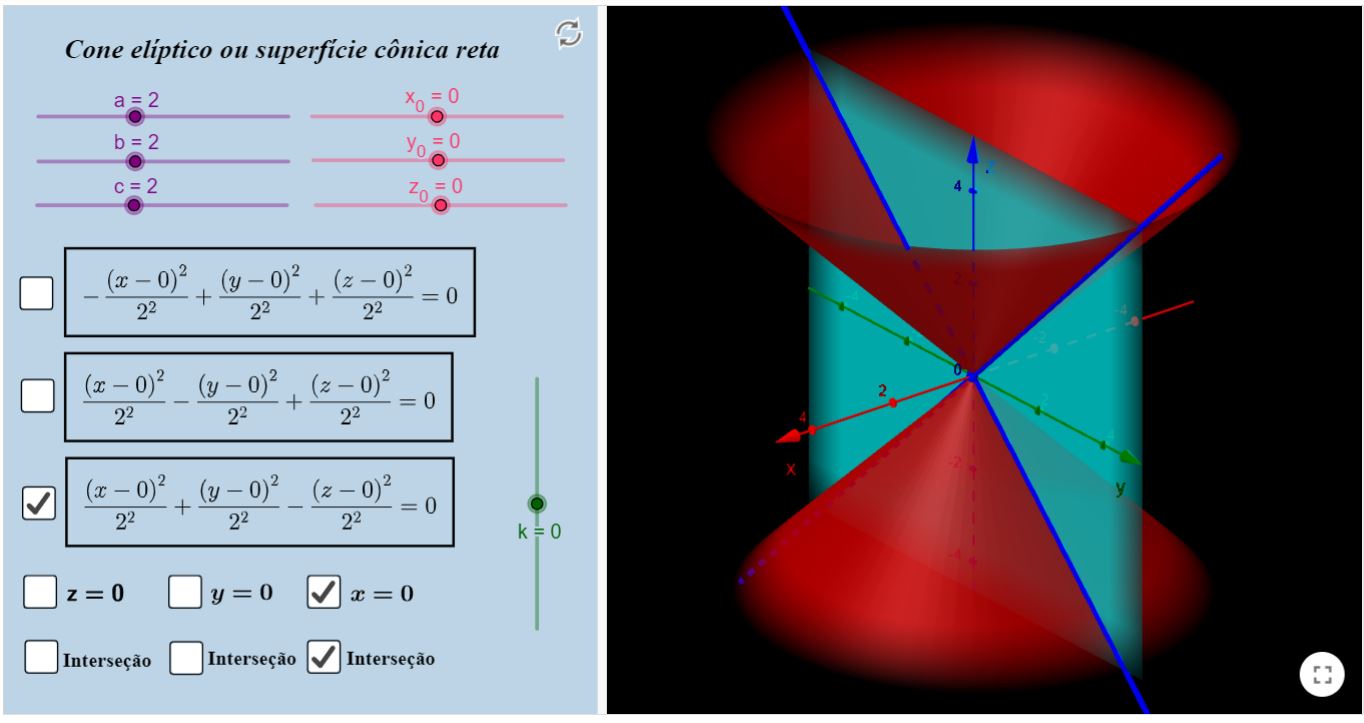
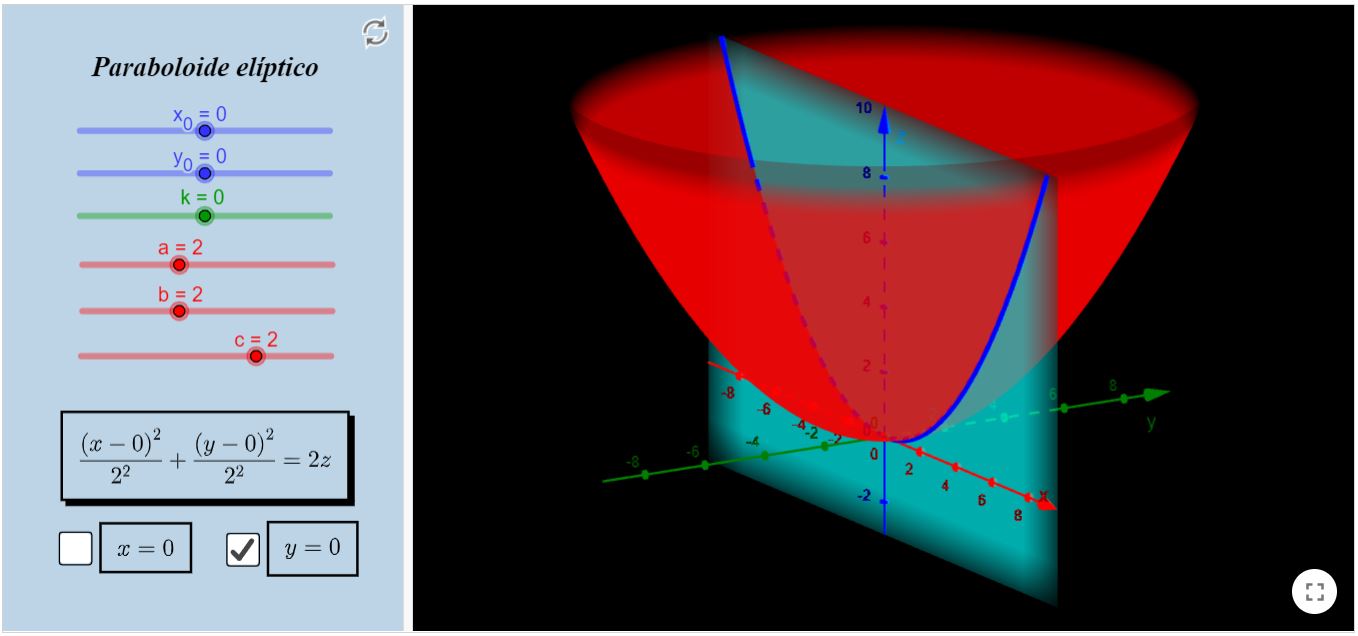
Paraboloide Elíptico
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a$ e $b$, eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$. O parâmetro $c$, por uma questão de limitação do programa, poderá assumir o valor 0 , mas observe que a superfície se torna uma degenerada.
Perceba que, ao abrir uma superfície, esta vem acompanhada de um plano que está pré-selecionado. Junto ao plano, está a curva da interseção das duas superfícies. Você pode controlar o plano através de $k$ (em verde). Existem outros paraboloides elípticos, mas esses são os mais comuns de serem vistos, por isso omitimos os outros neste subtópico.
Livro Geogebra

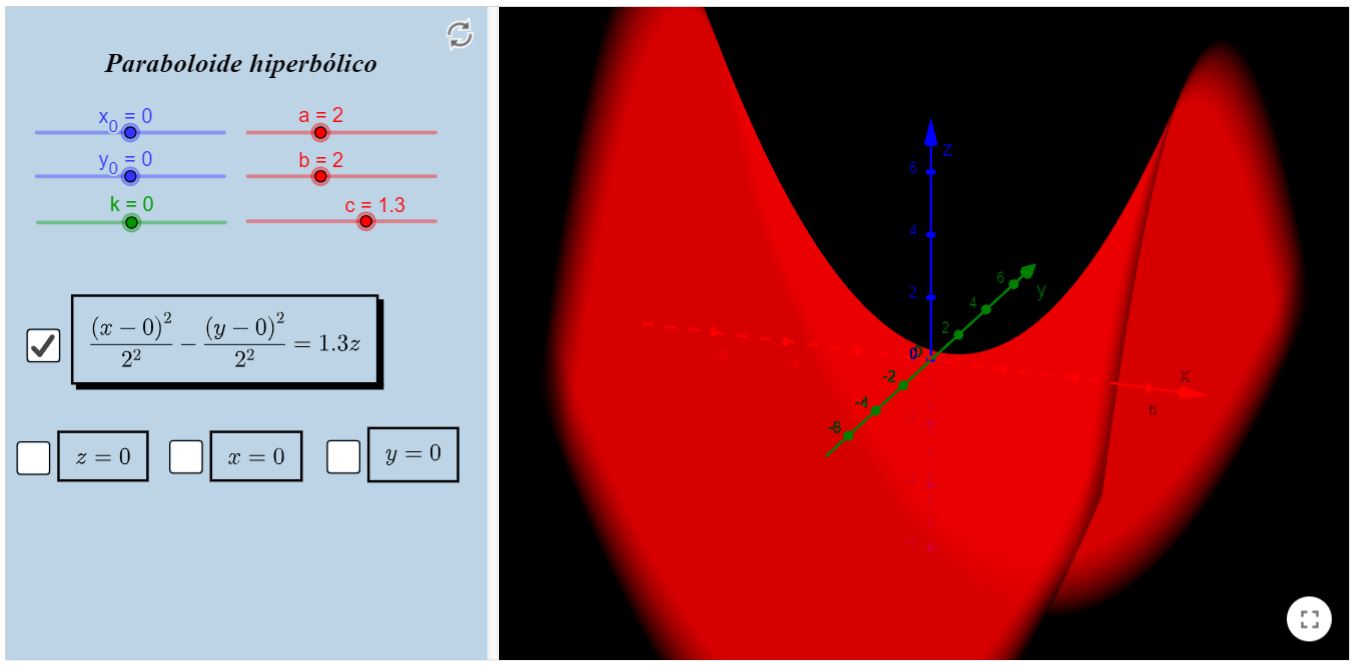
Paraboloide Hiperbólico
Sugerimos que selecione uma caixa por vez, por uma questão de clareza na visualização dos objetos. Preste atenção nos parâmetros $a$ e $b$ , eles estão configurados da mesma forma que foram supracitados, bem como $x_{0}, y_{0}$. O parâmetro $c$, por uma questão de limitação do programa, poderá assumir o valor 0 , mas observe que a superfície se torna uma degenerada.
Perceba que, ao abrir uma superfície, haverá a opção de selecionar três planos. Você pode, para cada plano, ver a interseção dele com a superfície já selecionada. Para cada opção de paraboloide, haverá três opções de planos, junto das suas respectivas interseções com a superfície. Inclusive poderá "mover" o plano alterando o valor de $k$ (em verde).
Livro Geogebra