Revisão de Geometria Analítica

Mudança de coordenadas esféricas

Relações entre coordenadas cartesianas e coordenadas esféricas
Para completar, temos as coordenadas esféricas, também usadas para melhor representar superfícies (de preferência, com natureza esférica). Diferentemente das coordenadas cilíndricas, agora há novos "integrantes", a saber:

  • $\rho >0$, o raio da esfera;
  • $\theta \in \left[0,2\pi \right]$, o ângulo percorrido no plano $XY$
  • $\varphi \in \left[0,\pi \right]$, o ângulo percorrido no semieixo positivo do eixo $-OZ$ ao semieixo negativo do eixo $-OZ$.
Note que, ao varrer completamente os ângulos $\theta$ e $\varphi$ (mantendo o raio $\rho $ constante), obteremos uma esfera de raio $\rho $. Talvez essa alusão tenha sido suficiente para justificar o porquê da variação de $\varphi$ não ser igual à variação de $\theta $.
Dado um ponto $P$ em coordenadas esféricas, ele será da forma $P=P\left(\rho ,\theta ,\varphi \right)$. Evidentemente, ele ainda existirá na forma cartesiana cotidiana, na forma $P=P\left(x,y,z\right)$. Ademais, as relações entre coordenadas são dadas por:
$x=\rho \cos \left(\theta \right)\text{sen}\left(\varphi \right)$
$y=\rho \text{sen}\left(\theta \right)\text{sen}\left(\varphi \right)$
$z=\rho \cos \left(\varphi \right)$
A partir delas, conseguimos chegar em outras duas relações, que também podem ser úteis:
$x=\rho \cos \left(\theta \right)\text{sen}\left(\varphi \right)\Rightarrow x^2=\rho ^2\cos ^2\left(\theta \right)\text{sen}^2\left(\varphi \right)$ $y=\rho \text{sen}\left(\theta \right)\text{sen}\left(\varphi \right)\Rightarrow y^2=\rho ^2\text{sen}^2\left(\theta \right)\text{sen}^2\left(\varphi \right)$ $z=\rho \cos \left(\varphi \right)\Rightarrow z^2=\rho ^2\cos ^2\left(\varphi \right)$
$x=\rho \cos \left(\theta \right)\text{sen}\left(\varphi \right)\Rightarrow \cos \left(\theta \right)=\frac{x}{\rho \text{sen}\left(\varphi \right)}$ $y=\rho \text{sen}\left(\theta \right)\text{sen}\left(\varphi \right)\Rightarrow \text{sen}\left(\theta \right)=\frac{y}{\rho \text{sen}\left(\varphi \right)}$ $\text{tg}\left(\theta \right)=\frac{y}{x}\Rightarrow \theta =\text{arctg}\left(\frac{y}{x}\right)$
Na segunda linha, consideramos $\varphi \ne 0\pm k\pi ,k\in \left\{0,1\right\}$, pois caso seja verdadeiro, teremos $\text{sen}\left(\varphi \right)=0\Rightarrow x=y=0$ e o ponto estará localizado sobre o eixo $-OZ$, isto é, não haverá necessidade de fazer cálculo pela fórmula.
Finalmente, temos que:
$\rho ^2=x^2+y^2+z^2\Rightarrow \rho =\sqrt{x^2+y^2+z^2}$
$\theta =\text{arctg}\left(\frac{y}{x}\right)$
$\varphi =\frac{z}{\sqrt{x^2+y^2+z^2}}$, pois $\cos \varphi =\frac{z}{\rho }$.
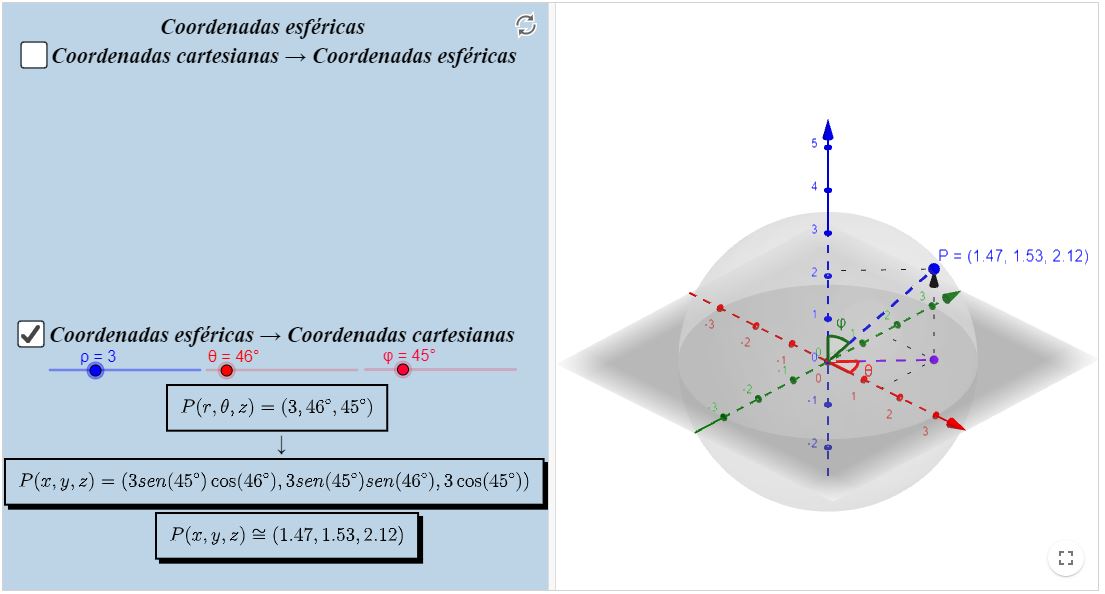
No recurso computacional, temos uma espécie de conversor de coordenadas esféricas em cartesianas e vice-versa. Sugerimos que selecione uma caixa de cada vez, para melhor visualização. Haverá uma esfera que contém o ponto desejado para que se tenha uma melhor visão da coordenada esférica. Pode ser que ela se torne mais interessante quando você começar a lidar com parametrização de superfícies (de naturezas esféricas, de preferência) ou integral de superfície. De qualquer forma, é importante saber as transformações.

Recursos computacionais

Parametrização de uma superfície cilíndrica I
Livro Geogebra