Revisão de Geometria Analítica

Mudança de coordenadas cilíndricas

Relações entre coordenadas cartesianas e coordenadas cilíndricas
Bem como em coordenadas polares, eventualmente é conveniente escrever pontos em coordenadas cilíndricas. Porém, desta vez isso será útil para descrever algumas superfícies. Esse novo sistema de coordenadas nada mais é que a junção do sistema de coordenadas polares com o eixo - $O Z$, nos permitindo viajar para o espaço.
Dado um ponto $P$ em coordenadas cilíndricas, ele será da forma $P=P(r, \theta, z)$. Obviamente, ele ainda existirá na forma cartesiana cotidiana, na forma $P=P(x, y, z)$. Ademais, as relações entre coordenadas são dadas por:

$x=r \cos (\theta)$	$\operatorname{sen}(\theta)$	$z=z$

A partir delas, conseguimos chegar em outras duas relações, que também podem ser úteis:

$x=r \cos (\theta) \Rightarrow x^{2}=r^{2} \cos ^{2}(\theta)$	$y=r \operatorname{sen}(\theta) \Rightarrow y^{2}=r^{2} \operatorname{sen}^{2}(\theta)$	$r^{2}=x^{2}+y^{2} \Rightarrow r=\sqrt{x^{2}+y^{2}}$
$x=r \cos (\theta) \Rightarrow \cos (\theta)=\frac{x}{r}$	$y=r \operatorname{sen}(\theta) \Rightarrow \operatorname{sen}(\theta)=\frac{y}{r}$	$\operatorname{tg}(\theta)=\frac{y}{x} \Rightarrow \theta=\operatorname{arctg}\left(\frac{y}{x}\right)$

No recurso computacional, temos uma espécie de conversor de coordenadas cilíndricas em cartesianas e vice-versa. Sugerimos que selecione uma caixa de cada vez, para melhor visualização. A malha que você vai encontrar pertence ao sistema $O X Y$, mas existe também a ilustração do ângulo $\theta$ e o segmento que simboliza $r$, para facilitar a outra concepção do ponto também.

Recursos computacionais

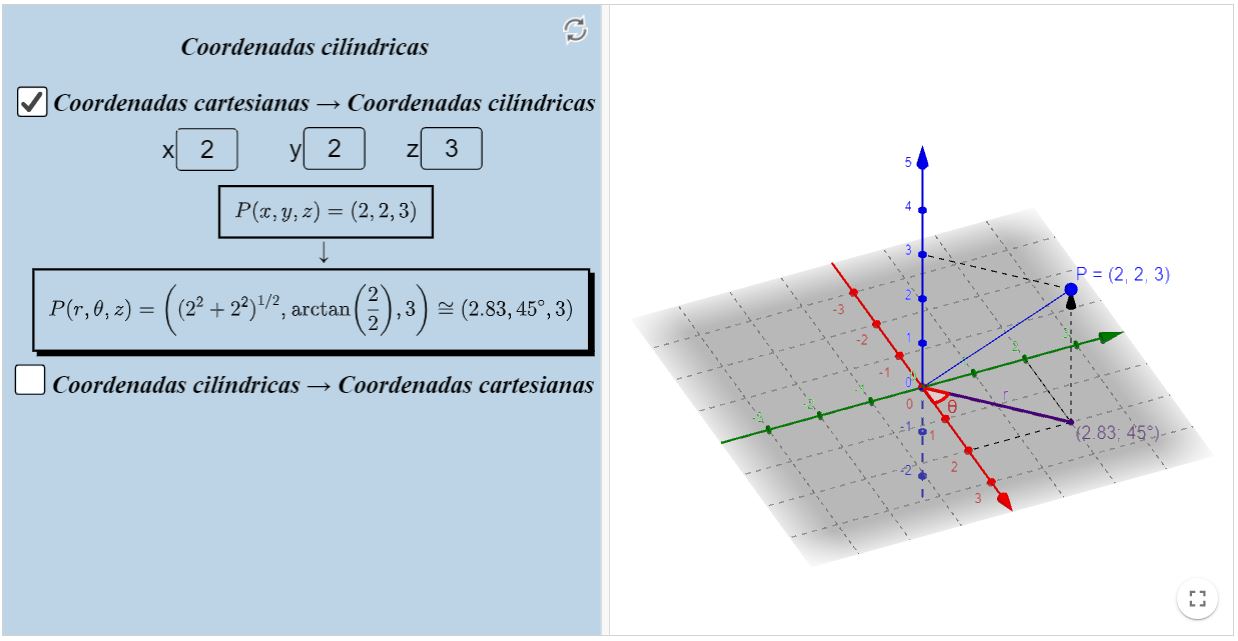
Mudança de coordenadas cilíndricas
Livro Geogebra