Revisão de Geometria Analítica
Equações paramétricas da reta no espaço
Uma parametrização da reta
Equação paramétrica de uma reta no espaço dados um ponto e um vetor paralelo a ela.
Definição
Dados $P_{0}, v \in \mathbb{R}^{3}$ tais que $P_{0}$ pertence à reta $r$ e $v$ é um vetor paralelo (ou vetor diretor de $r$ ),
a equação paramétrica de $r$ é dada por:
$r:(x, y, z)=P_{0}+t v, t \in \mathbb{R}$.
Recursos computacionais
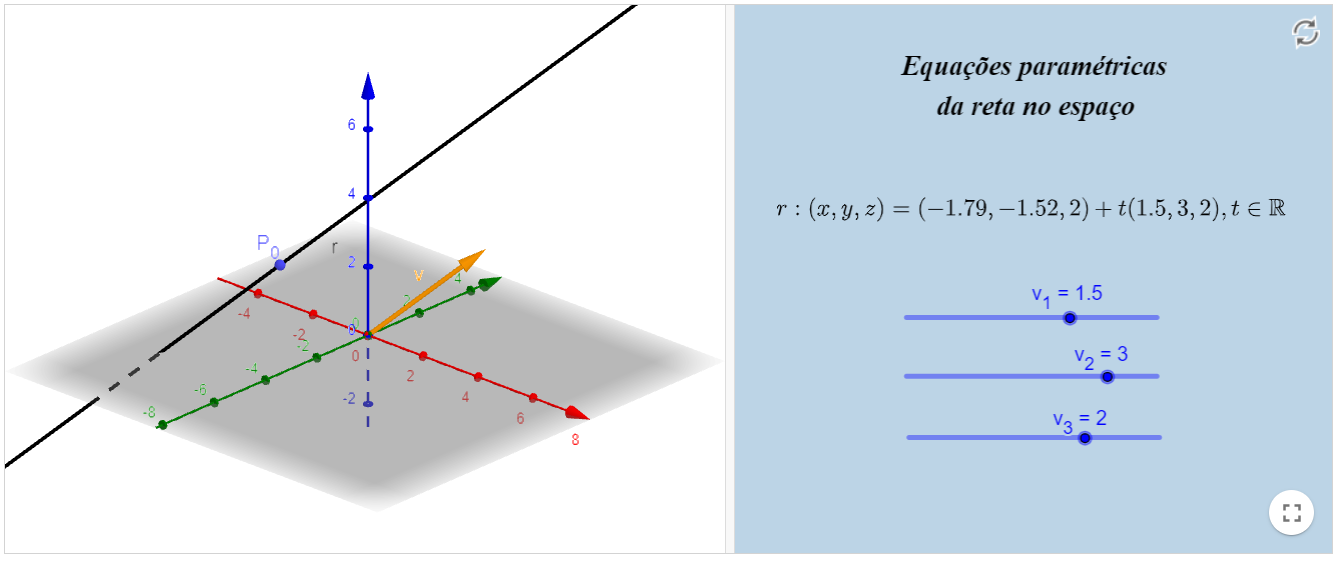
Aqui abaixo, é possível encontrar um exemplo de reta no espaço definida de forma paramétrica. Perceba que o eixo em vermelho corresponde ao eixo $x$, o verde corresponde ao
eixo $y$ e o azul corresponde ao eixo $z$. Além disso, você pode mudar as coordenadas do vetor diretor $v=\left(v_{1}, v_{2}, v_{3}\right)$ através do ponto deslizante e mudar
as coordenadas do ponto $P_{0}$ pertencente à reta, basta clicar na caixa do ponto e inserir novas coordenadas na forma $((x, y, z))$.
Equação Paramétrica da Reta no Espaço
Livro Geogebra